题目内容
14. 已知,点B、C是双曲线y=$\frac{4}{x}$在第一象限分支上的两点,点A在x轴正半轴上,△AOB为等腰直角三角形,∠B=90°,AC垂直于x轴.
已知,点B、C是双曲线y=$\frac{4}{x}$在第一象限分支上的两点,点A在x轴正半轴上,△AOB为等腰直角三角形,∠B=90°,AC垂直于x轴.(1)求点C的坐标;
(2)点D为x轴上一点,当△BCD为等腰三角形时,求点D的坐标.
分析 (1)过点B作BH⊥OA于点H,根据△AOB是等腰直角三角形得出BH=OH=$\frac{1}{2}$OA.设B(a,a)(a>0),由点B在双曲线y=$\frac{4}{x}$上求出a的值,故可得出B点坐标,进而可得出A点坐标,设C(4,y).根据点C在双曲线上即可得出y的值;
(2)设D(x,0),用x表示出BC2,BD2,CD2的值,再分BC=BD,BC=CD或BD=CD三种情况进行讨论即可.
解答  解:(1)过点B作BH⊥OA于点H,
解:(1)过点B作BH⊥OA于点H,
∵△AOB是等腰直角三角形,∠B=90°,
∴BH=OH=$\frac{1}{2}$OA.
∵点B在第一象限,
∴设B(a,a)(a>0).
∵点B在双曲线y=$\frac{4}{x}$上,
∴a2=4,
∴a=2或a=-2(不合题意,舍去),
∴B(2,2),
∴A(4,0).
∵AC⊥x轴,
∴设C(4,y),
∵点C在双曲线y=$\frac{4}{x}$上,
∴C(4,1);
(2)∵设D(x,0),
∴BC2=5,BD2=x2-4x+8,CD2=x2-8x+17,
当△BCD是等腰直角三角形时,BC=BD,BC=CD或BD=CD.
当BC=BD,即BC2=BD2时,x2-4x+8=5,解得x=1或x=3,
∴D(1,0)或(3,0);
当BC=CD,即BC2=CD2时,x2-8x+17=5,解得x=2或x=6,
当D(6,0)时,BC=CD=$\sqrt{5}$,BD=2$\sqrt{5}$,
∴BC+CD=BD,不能构成三角形,
∴x=6不合题意,
∴D(2,0);
当BD=CD,即BD2=CD2,x2-4x+8=x2-8x+17,解得x=$\frac{9}{4}$,
∴D($\frac{9}{4}$,0).
综上所述,D(1,0),(3,0),(2,0),($\frac{9}{4}$,0).
点评 本题考查的是反比例函数综合题,涉及到反比例函数图象上点的坐标特点、等腰直角三角形的性质等知识,在解答(2)时要注意进行分类讨论.

| A. |  | B. |  | C. |  | D. |  |
| A. | 经过已知点P和Q的圆的圆心轨迹是线段PQ的垂直平分线 | |
| B. | 到点A的距离等于2cm的点的轨迹是以点A为圆心,2cm长为半径的圆 | |
| C. | 与直线AB距离为3的点的轨迹是平行于直线AB且和AB距离为3的两条直线 | |
| D. | 以线段AB为底边的等腰三角形两底角平分线交点的轨迹是线段AB的垂直平分线 |
| A. | 3.019×107 | B. | 3.018×108 | C. | 30.2×106 | D. | 3.02×107 |
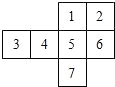 将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,应剪去(序号)( )
将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,应剪去(序号)( )| A. | 1或2或3 | B. | 3或4或5 | C. | 4或5或6 | D. | 1或2或6 |
 如图,∠AOB=124°,OC是∠AOB的平分线,∠1与∠2互余,求∠1和∠BOD的度数.
如图,∠AOB=124°,OC是∠AOB的平分线,∠1与∠2互余,求∠1和∠BOD的度数. 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,3),B(-3,n)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,3),B(-3,n)两点.