题目内容
18. 如图所示,A、B两地相距308km,飞机从A地飞往B地,因风向关系使飞机偏离航线6°,飞行115km到达C地,求此时飞机从C地到B地的距离,及其航向与CB方向的偏角α(精确到0.01).
如图所示,A、B两地相距308km,飞机从A地飞往B地,因风向关系使飞机偏离航线6°,飞行115km到达C地,求此时飞机从C地到B地的距离,及其航向与CB方向的偏角α(精确到0.01).
分析 延长AC,过B点作垂线与AC延长线相交于点D,根据sinA=$\frac{BD}{AB}$,求出BD,根据cosA=$\frac{AD}{AB}$,求出AD,从而求出CD,根据tanα=$\frac{BD}{CD}$求出α,最后根据sinα=$\frac{BD}{BC}$,求出BC即可得出答案.
解答 解:延长AC,过B点作垂线与AC延长线相交于点D,
∵sinA=$\frac{BD}{AB}$,
∴BD=ABsin6°≈308×0.1045=32.186,
∵cosA=$\frac{AD}{AB}$,
∴AD=ABcos6°≈308×0.9945≈306.306,
∵AC=115,
∴CD=306.306-115=191.306,
∴tanα=$\frac{BD}{CD}$=$\frac{32.186}{191.306}$≈0.17,
∴α=9.6°,
∵sinα=$\frac{BD}{BC}$,
∴BC=$\frac{BD}{sinα}$=$\frac{32.186}{0.167}$≈192.73,
答:此时飞机从C地到B地的距离是192.73km,航向与CB方向的偏角α=9.6°.
点评 本题主要考查了解直角三角形的应用-方向角问题,用到的知识点是方向角含义,正确记忆三角函数的定义是解决本题的关键.

练习册系列答案
相关题目
8. 如图,在△ABC中,AB的垂直平分线DE,AD=6,△AEC的周长为15,那么△ABC的周长为( )
如图,在△ABC中,AB的垂直平分线DE,AD=6,△AEC的周长为15,那么△ABC的周长为( )
 如图,在△ABC中,AB的垂直平分线DE,AD=6,△AEC的周长为15,那么△ABC的周长为( )
如图,在△ABC中,AB的垂直平分线DE,AD=6,△AEC的周长为15,那么△ABC的周长为( )| A. | 15 | B. | 21 | C. | 27 | D. | 33 |
3.若点P(-a,4-a)是第二象限的点,则a的取值范围是( )
| A. | a<4 | B. | a>4 | C. | a<0 | D. | 0<a<4 |
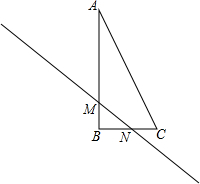 如图,在直角三角形ABC中,∠B=90°,点M,N分别在边AB,BC上,且BM=BN,
如图,在直角三角形ABC中,∠B=90°,点M,N分别在边AB,BC上,且BM=BN, 小李是一位集邮爱好者,2014年年底,他收藏的邮票数量达到了100枚,到2015年年底达到了200枚,他绘制了一幅如图所示的统计图来表示他的收藏量,合适吗?为什么?
小李是一位集邮爱好者,2014年年底,他收藏的邮票数量达到了100枚,到2015年年底达到了200枚,他绘制了一幅如图所示的统计图来表示他的收藏量,合适吗?为什么?