题目内容
7.已知3x-4y-z=0,2x+y-8z=0,求$\frac{{x}^{2}+{y}^{2}-{z}^{2}}{xy+xz+2yz}$的值.分析 解关于x和y的方程组$\left\{\begin{array}{l}{3x-4y-z=0}\\{2x+y-8z=0}\end{array}\right.$,利用z表示出x和y,然后代入所求的分式进行化简求解.
解答 解:解关于x和y的方程组$\left\{\begin{array}{l}{3x-4y-z=0}\\{2x+y-8z=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=3z}\\{y=2z}\end{array}\right.$,
则原式=$\frac{9{z}^{2}+4{z}^{2}-{z}^{2}}{6{z}^{2}+3{z}^{2}+4{z}^{2}}$=$\frac{12{z}^{2}}{13{z}^{2}}$=$\frac{12}{13}$.
点评 本题考查了方程组的解法以及分式的化简求值,正确解关键x和y的方程组是关键.

练习册系列答案
相关题目
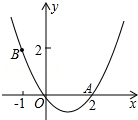 如图,抛物线y=ax2+bx(a>0)经过点A(2,0)和点B(-1,2).
如图,抛物线y=ax2+bx(a>0)经过点A(2,0)和点B(-1,2). 如图所示,A、B两地相距308km,飞机从A地飞往B地,因风向关系使飞机偏离航线6°,飞行115km到达C地,求此时飞机从C地到B地的距离,及其航向与CB方向的偏角α(精确到0.01).
如图所示,A、B两地相距308km,飞机从A地飞往B地,因风向关系使飞机偏离航线6°,飞行115km到达C地,求此时飞机从C地到B地的距离,及其航向与CB方向的偏角α(精确到0.01). 如图,点B、C为直线AD上的点,点E、F分别在直线AD的两侧,且AE=DF,AE∥DF,AB=DC.
如图,点B、C为直线AD上的点,点E、F分别在直线AD的两侧,且AE=DF,AE∥DF,AB=DC.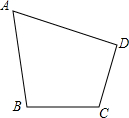 在四边形ABCD中,∠A=60°,AB⊥BC,AD⊥DC,AB=20cm,CD=10cm,求AD、BC的长.(保留根号)
在四边形ABCD中,∠A=60°,AB⊥BC,AD⊥DC,AB=20cm,CD=10cm,求AD、BC的长.(保留根号) 如图,CD⊥AB于D,GF⊥AB于F,∠1=50°,求∠2度数.
如图,CD⊥AB于D,GF⊥AB于F,∠1=50°,求∠2度数.