题目内容
1.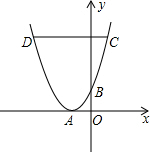 如图,在平面直角坐标系中,抛物线的顶点A(-1,0)在x轴上,与y轴交于点B,点C(1,4)为抛物线上一点,CD∥x轴交抛物线于点D.
如图,在平面直角坐标系中,抛物线的顶点A(-1,0)在x轴上,与y轴交于点B,点C(1,4)为抛物线上一点,CD∥x轴交抛物线于点D.(1)求抛物线的解析式;
(2)点P为抛物线对称轴左侧图象上一动点,设点P的横坐标为t,△PBC的面积为S,求S与t的函数关系式;
(3)在(2)的条件下,作直线AE⊥x轴,交线段CD于点E,连接AP、PE,当∠APE=90°时,求tan∠PCE的值.
分析 (1)根据题意设为顶点式代入点C即可求解;
(2)连接PC,PB,BC,过点P作平行于x轴的直线交BC于点Q,运用点P的横坐标为t,表示纵坐标y=t2+2t+1,进一步表示线段PQ的长度,利用△PBC的面积S=S△PCQ+S△PQB即可求解;
(3)过点P作平行于y轴的直线,交x轴于点M,交CD于点H,构造相似三角形△HPE∽△MAP,运用对应边的比相等$\frac{PH}{AM}=\frac{HE}{PM}$,建立等量关系$\frac{3-{(t}^{2}+2t)}{-1-t}$=$\frac{-1-t}{{t}^{2}+2t+1}$,进一步求解即可.
解答 解:(1)由抛物线的顶点A(-1,0),设抛物线为:y=a(x+1)2,
把点C(1,4)的坐标代入得:4=a(1+1)2,
解得:a=1,
∴y=(x+1)2,
抛物线的解析式为:y=x2+2x+1.
(2)如图1,连接PC,PB,BC,过点P作平行于x轴的直线交BC于点Q,
y=x2+2x+1,当x=0,y=1,∴点B(0,1),
设直线BC解析式为:y=mx+n,
把点B(0,1),和点C(1,4)代入得:$\left\{\begin{array}{l}{4=m+n}\\{1=n}\end{array}\right.$
解得:$\left\{\begin{array}{l}{m=3}\\{n=1}\end{array}\right.$,
∴y=3x+1,
设点P的横坐标为t,则纵坐标为:t2+2t+1,
把y=t2+2t+1代入y=3x+1,
得:x=$\frac{{t}^{2}+2t}{3}$,
∴PQ=$\frac{{t}^{2}+2t}{3}$-t=$\frac{{t}^{2}-t}{3}$,
∴△PBC的面积为S=S△PCQ+S△PQB=$\frac{1}{2}$×PQ×[4-(t2+2t+1)+(t2+2t+1)-1]=$\frac{1}{2}$×PQ×(4-1)=$\frac{1}{2}$×$\frac{{t}^{2}-t}{3}$×3=$\frac{1}{2}$t2-$\frac{1}{2}$t,
∴S=$\frac{1}{2}$t2-$\frac{1}{2}$t.
(3)如图2,过点P作平行于y轴的直线,交x轴于点M,交CD于点H,
∵CD∥x轴,
∴PH⊥CD,PM⊥x轴,
∴∠PHE=∠AMP=90°,
∵∠APE=90°,
∴∠HPE+∠APM=90°,
∵∠HPE+∠PEH=90°,
∴∠APM=∠PEH,
∴△HPE∽△MAP,
∴$\frac{PH}{AM}=\frac{HE}{PM}$,
由(2)点P(t,t2+2t+1),
∴AM=-1-t,PM=t2+2t+1,
∵CD∥x轴,点C(1,4),
∴PH=4-(t2+2t+1)=3-(t2+2t),
HE=AM=-1-t,
∴$\frac{3-{(t}^{2}+2t)}{-1-t}$=$\frac{-1-t}{{t}^{2}+2t+1}$,
解得:t=-1-$\sqrt{3}$,或t=-1+$\sqrt{3}$(舍去),
∴PH=3-(t2+2t)=1,
CH=1-(-1-$\sqrt{3}$)=2+$\sqrt{3}$,
在直角三角形PHE中:tan∠PCE=$\frac{PH}{CH}$=$\frac{1}{2+\sqrt{3}}$=2-$\sqrt{3}$.
点评 此题考查了待定系数法求解析式,灵活运用顶点式是求解析式的关键;在解决形积问题时,会运用坐标表示线段,会运用已知建立数量关系是解题的关键.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案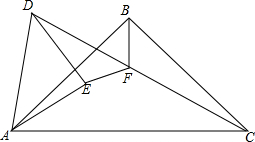 如图,等腰直角△ABC中,∠ABC=90°,等腰直角△ADE中,∠AED=90°,AE<AB,点E在△ABC内部,点F是CD的中点,猜想EF和BF的数量和位置关系,并说明理由.
如图,等腰直角△ABC中,∠ABC=90°,等腰直角△ADE中,∠AED=90°,AE<AB,点E在△ABC内部,点F是CD的中点,猜想EF和BF的数量和位置关系,并说明理由.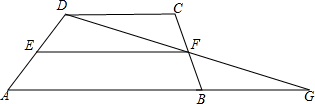 如图:已知梯形ABCD中,AB∥CD,E,F分别为AD,BC的中点,连结DF并延长交AB的延长线于点G,请解答下列问题:
如图:已知梯形ABCD中,AB∥CD,E,F分别为AD,BC的中点,连结DF并延长交AB的延长线于点G,请解答下列问题: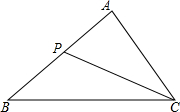 如图,已知△ACP∽△ABC,AC=6,AP=3,则AB的长为12.
如图,已知△ACP∽△ABC,AC=6,AP=3,则AB的长为12.