题目内容
1.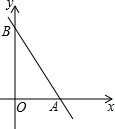 如图,在平面直角坐标系xOy中,直线AB过点A(3,0)、B(0,m)(m>0),tan∠BAO=2.
如图,在平面直角坐标系xOy中,直线AB过点A(3,0)、B(0,m)(m>0),tan∠BAO=2.(1)求直线AB的表达式;
(2)反比例函数y=$\frac{k_1}{x}$的图象与直线AB交于第一象限内的C、D两点(BD<BC),当AD=2DB时,求k1的值;
(3)设线段AB的中点为E,过点E作x轴的垂线,垂足为点M,交反比例函数y=$\frac{k_2}{x}$的图象于点F,分别联结OE、OF,当△OEF∽△OBE时,请直接写出满足条件的所有k2的值.
分析 (1)先通过解直角三角形求得A的坐标,然后根据待定系数法即可求得直线AB的解析式;
(2)作DE∥OA,根据题意得出$\frac{DE}{OA}$=$\frac{BD}{AB}$=$\frac{1}{3}$,求得DE,即D的横坐标,代入AB的解析式求得纵坐标,然后根据反比例函数图象上点的坐标特征即可求得k1;
(3)根据勾股定理求得AB、OE,进一步求得BE,然后根据相似三角形的性质求得EF的长,从而求得FM的长,得出F的坐标,然后根据反比例函数图象上点的坐标特征即可求得k2.
解答 解:(1)∵A(3,0)、B(0,m)(m>0),
∴OA=3,OB=m,
∵tan∠BAO=$\frac{OB}{OA}$=2,
∴m=6,
设直线AB的解析式为y=kx+b,
代入A(3,0)、B(0,6)得:$\left\{\begin{array}{l}{0=3k+b}\\{6=b}\end{array}\right.$
解得:b=6,k=-2
∴直线AB的解析式为y=-2x+6;
(2)如图1,∵AD=2DB,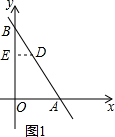 ∴$\frac{DB}{AB}$=$\frac{1}{3}$,
∴$\frac{DB}{AB}$=$\frac{1}{3}$,
作DE∥OA,
∴$\frac{DE}{OA}$=$\frac{BD}{AB}$=$\frac{1}{3}$,
∴DE=$\frac{1}{3}$OA=1,
∴D的横坐标为1,
代入y=-2x+6得,y=4,
∴D(1,4),
∴k1=1×4=4;
(3)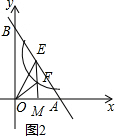 如图2,∵A(3,0),B(0,6),
如图2,∵A(3,0),B(0,6),
∴E($\frac{3}{2}$,3),AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=3$\sqrt{5}$,
∵OE是Rt△OAB斜边上的中线,
∴OE=$\frac{1}{2}$AB=$\frac{3}{2}$$\sqrt{5}$,BE=$\frac{3}{2}$$\sqrt{5}$,
∵EM⊥x轴,
∴F的横坐标为$\frac{3}{2}$,
∵△OEF∽△OBE,
∴$\frac{EF}{BE}$=$\frac{OE}{OB}$,
∴$\frac{EF}{\frac{3}{2}\sqrt{5}}=\frac{\frac{3}{2}\sqrt{5}}{6}$,
∴EF=$\frac{15}{8}$,
∴FM=3-$\frac{15}{8}$=$\frac{9}{8}$.
∴F($\frac{3}{2}$,$\frac{9}{8}$),
∴k2=$\frac{3}{2}$×$\frac{9}{8}$=$\frac{27}{16}$.
点评 本题是反比例函数的综合题,考查了待定系数法求一次函数的解析式,反比例函数图象上点的坐标特征,三角形相似的性质以及勾股定理的应用,求得关键点的坐标是解题的关键.

| A. | 7.6×107克 | B. | 7.6×10-6克 | C. | 7.6×10-7克 | D. | 7.6×10-8克 |
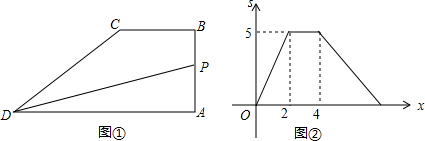
| A. | 4 | B. | 2+$\sqrt{13}$ | C. | 5 | D. | 4+$\sqrt{13}$ |
| A. | $\sqrt{8}$ | B. | $\sqrt{12}$ | C. | $\sqrt{30}$ | D. | $\sqrt{\frac{1}{2}}$ |
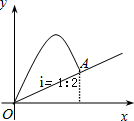 如图,小亮从斜坡的点O处抛出一个沙包,沙包轨迹抛物线的解析式为y=12x-x2,斜坡OA的坡度i=1:2,则沙包在斜坡的落点A的垂直高度是$\frac{23}{4}$.
如图,小亮从斜坡的点O处抛出一个沙包,沙包轨迹抛物线的解析式为y=12x-x2,斜坡OA的坡度i=1:2,则沙包在斜坡的落点A的垂直高度是$\frac{23}{4}$.