题目内容
18. 如图,已知矩形ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F.若AB=4,BC=8,求四边形AFCE的面积.
如图,已知矩形ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F.若AB=4,BC=8,求四边形AFCE的面积.
分析 由ASA证明△AOE≌△COF,得出对应边相等EO=FO,证出四边形AFCE为平行四边形,再由FE⊥AC,即可得出平行四边形AFCE为菱形,然后再利用勾股定理计算出AC和EF的长,进而可得四边形AFCE的面积.
解答 解:∵四边形ABCD是矩形,
∴AE∥FC,
∴∠EAO=∠FCO,
∵EF垂直平分AC,
∴AO=CO,FE⊥AC,
在△AOE和△COF中,
$\left\{\begin{array}{l}{∠EAO=∠FCO}\\{AO=CO}\\{∠AOE=∠COF}\end{array}\right.$,
∴△AOE≌△COF(ASA),
∴EO=FO,
∴四边形AFCE为平行四边形,
又∵FE⊥AC,
∴平行四边形AFCE为菱形.
∴AF=FC,
设BF=x,则CF=AF=8-x,
在Rt△ABF中,AB2+BF2=AF2,
∴42+x2=(8-x)2,
解得:x=3,
∴FC=5,
在Rt△ABC中,AC=$\sqrt{{4}^{2}+{8}^{2}}$=4$\sqrt{5}$,
∴CO=2$\sqrt{5}$,
在Rt△FCO中,FO=$\sqrt{F{C}^{2}-C{O}^{2}}$=$\sqrt{25-20}$=$\sqrt{5}$,
∴EF=2$\sqrt{5}$,
∴四边形AFCE的面积为;$\frac{1}{2}$×2$\sqrt{5}$×4$\sqrt{5}$=20.
点评 此题主要考查了菱形的判定和菱形的面积,关键是掌握对角线互相垂直的平行四边形是菱形,菱形的面积等于对角线之积的一半.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
8.与$\sqrt{5}$最接近的整数是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
13.政府去年对某校的投资为2百万元,预计今明两年的投资总额为8百万元,设政府对该校这两年投资的平均增长率为x,则可列方程为( )
| A. | 2(1+x)2=4 | B. | 2(1+x)2=8 | C. | 2(x+2)2=8 | D. | 2(x+1)(x+2)=8 |
10.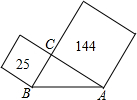 如图,已知在直角三角形ABC中,以直角边BC、AC为边的正方形的面积分别为25、144,则AB的长为( )
如图,已知在直角三角形ABC中,以直角边BC、AC为边的正方形的面积分别为25、144,则AB的长为( )
 如图,已知在直角三角形ABC中,以直角边BC、AC为边的正方形的面积分别为25、144,则AB的长为( )
如图,已知在直角三角形ABC中,以直角边BC、AC为边的正方形的面积分别为25、144,则AB的长为( )| A. | 169 | B. | 119 | C. | 13 | D. | 17 |
 如图,在?ABCD中,点F在边AD上,BF交AC于点E,过点E作EG∥BC交AB于点G,若AF:FD=2:1,求GE:BC的值.
如图,在?ABCD中,点F在边AD上,BF交AC于点E,过点E作EG∥BC交AB于点G,若AF:FD=2:1,求GE:BC的值. 如图,正方形ABCD中,AC,BD相交于点O,AE平分∠BAC交BD于E.
如图,正方形ABCD中,AC,BD相交于点O,AE平分∠BAC交BD于E.