题目内容
16.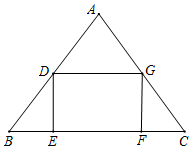 如图,在△ABC中,AB=AC=10,BC=12,矩形DEFG的顶点位于△ABC的边上,设EF=x,S四边形DEFG=y.
如图,在△ABC中,AB=AC=10,BC=12,矩形DEFG的顶点位于△ABC的边上,设EF=x,S四边形DEFG=y.(1)填空:自变量x的取值范围是0<x<12;
(2)求出y与x的函数表达式;
(3)请描述y随x的变化而变化的情况.
分析 (1)根据题意即可得到结论;
(2)利用勾股定理和等腰三角形的三线合一求得BN、AN,再利用△ADG∽△ABC,得出比例线段,利用x表示出MN,进一步利用矩形的面积求的函数解析式;列表取值,描点画出图象;
(3)根据以上三种表示方式回答问题即可.
解答 解:(1)0<x<12;
故答案为:0<x<12;
(2)如图,过点A作AN⊥BC于点N,交DG于点M,
∵AB=AC=10,BC=12,AN⊥BC,
∴BN=CN=6,AN=$\sqrt{A{B}^{2}-B{N}^{2}}$=8,
∵DG∥BC,
∴∠ADG=∠ABC,∠AGD=∠ACB,
∴△ADG∽△ABC,
$\frac{AM}{AN}=\frac{EF}{BC}$,即$\frac{8-MN}{8}=\frac{x}{12}$,
∴MN=8-$\frac{2}{3}$x.
∴y=EF•MN=x(8-$\frac{2}{3}$x)=-$\frac{2}{3}$x2+8x=-$\frac{2}{3}$(x-6)2+24;
(3)当0<x<6时,y随x的增大而增大;
当x=6时,y的值达到最大值24,
当6<x<12时,y随x的增大而减小.
点评 此题考查二次函数的运用,利用相似三角形的性质、矩形的面积求得函数解析式是解决问题的关键.

练习册系列答案
相关题目
6.已知A(x1,y1),B(x2,y2)是反比例函数y=-$\frac{{k}^{2}}{x}$图象上的两个点,且x1<x2,则y1与y2的大小关系是( )
| A. | y1<y2 | B. | y1=y2 | C. | y1>y2 | D. | 大小不确定 |
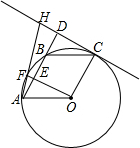 如图A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作OF的平行线交AB的延长线于点D,延长AF交直线CD于点H.
如图A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作OF的平行线交AB的延长线于点D,延长AF交直线CD于点H.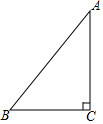 如图,已知Rt△ABC,∠C=90°,AC≠BC.
如图,已知Rt△ABC,∠C=90°,AC≠BC.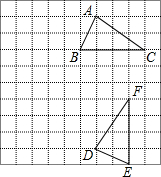 如图,在小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,根据图形解答下列问题:
如图,在小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,根据图形解答下列问题: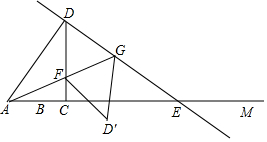 如图,射线AM上有一点B,AB=6,点C是射线AM上异于B的一点,过C作CD⊥AM,且CD=$\frac{4}{3}$AC,过D点作DE⊥AD,交射线AM于E,在射线CD取点F,使得CF=CB,连接AF并延长,交DE于点G,设AC=3x.
如图,射线AM上有一点B,AB=6,点C是射线AM上异于B的一点,过C作CD⊥AM,且CD=$\frac{4}{3}$AC,过D点作DE⊥AD,交射线AM于E,在射线CD取点F,使得CF=CB,连接AF并延长,交DE于点G,设AC=3x.