题目内容
12. 如图,矩形ABCD中,点E、F分别在边CD、AB上,且DE=BF.
如图,矩形ABCD中,点E、F分别在边CD、AB上,且DE=BF.(1)求证:四边形AFCE是平行四边形.
(2)若四边形AFCE是菱形,AB=8,AD=4,求菱形AFCE的周长.
分析 (1)由矩形的性质得出AB∥CD,AB=CD,∠B=90°,证出AF=CE,即可得出四边形AFCE是平行四边形.
(2)由菱形的性质得出AF=FC=CE=AE,BC=AD=4,设AF=CF=x,则BF=8-x,在Rt△BCF中,由勾股定理得出方程,解方程即可.
解答 (1)证明:∵四边形ABCD是矩形,
∴AB∥CD,AB=CD,∠B=90°,
∵DE=BF,
∴AF=CE,
∴四边形AFCE是平行四边形.
(2)∵四边形AFCE是菱形,
∴AF=FC=CE=AE,BC=AD=4,
设AF=CF=x,则BF=8-x,
在Rt△BCF中,由勾股定理得:(8-x)2+42=x2,
解得:x=5,
∴AF=FC=CE=AE=5,
∴菱形AFCE的周长=4×5=20.
点评 此题考查了菱形的性质、矩形的性质、平行四边形的判定以及勾股定理.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
20. 如图所示的几何体的左视图( )
如图所示的几何体的左视图( )
 如图所示的几何体的左视图( )
如图所示的几何体的左视图( )| A. |  | B. |  | C. |  | D. |  |
17.下列计算正确的是( )
| A. | 20a+17c=37ac | B. | (x2y)3=x5y3 | ||
| C. | x3÷x6=x3 | D. | (a+b-1)2=a2+b2+1+2ab-2a-2b |
1.下列命题中,真命题的是( )
| A. | 两条直线平行,同旁内角相等 | B. | 内错角相等 | ||
| C. | 同位角相等 | D. | 对顶角相等 |
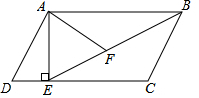 如图,在?ABCD中 过点A作AE⊥DC,垂足为E,连接BE,F为BE上一点,且∠AFE=∠D.
如图,在?ABCD中 过点A作AE⊥DC,垂足为E,连接BE,F为BE上一点,且∠AFE=∠D.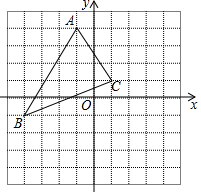 如图,在平面直角坐标系中,A(-1,4),B(-4,-1),C(1,1).
如图,在平面直角坐标系中,A(-1,4),B(-4,-1),C(1,1).