题目内容
1.下列命题中,真命题的是( )| A. | 两条直线平行,同旁内角相等 | B. | 内错角相等 | ||
| C. | 同位角相等 | D. | 对顶角相等 |
分析 分析是否为真命题,需要分别分析各题设是否能推出结论,从而利用排除法得出答案.
解答 解:A、两条直线平行,同旁内角互补,故A不符合题意;
B、内错角不一定相等,故B不符合题意;
C、同位角不一定相等,故C不符合题意;
D、对顶角相等,故D符合题意;
故选:D.
点评 主要考查命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.在实数$\frac{\sqrt{2}}{2}$,-$\root{3}{8}$,3.14,0中,无理数是( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | -$\root{3}{8}$ | C. | 3.14 | D. | 0 |
6.下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
| 甲 | 乙 | 丙 | 丁 | |
| 平均数(cm) | 180 | 185 | 185 | 180 |
| 方差 | 3.6 | 3.6 | 7.4 | 8.1 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
10.某公司从2014年开始投入技术改进资金,经技术改进后,其产品的成本不断降低,具体数据如下表:
(1)请你认真分析表中数据,从一次函数和反比例函数中确定哪一个函数能表示其变化规律,给出理由,并求出其解析式;
(2)按照这种变化规律,若2017年已投入资金5万元.
①预计生产成本每件比2016年降低多少万元?
②若打算在2017年把每件产品成本降低到3.2万元,则还需要投入技改资金多少万元?(结果精确到0.01万元).
| 年 度 | 2013 | 2014 | 2015 | 2016 |
| 投入技改资金x(万元) | 2.5 | 3 | 4 | 4.5 |
| 产品成本y(万元/件) | 7.2 | 6 | 4.5 | 4 |
(2)按照这种变化规律,若2017年已投入资金5万元.
①预计生产成本每件比2016年降低多少万元?
②若打算在2017年把每件产品成本降低到3.2万元,则还需要投入技改资金多少万元?(结果精确到0.01万元).
11. 如图,点O在直线AB上,若∠BOC=60°,则∠AOC的大小是( )
如图,点O在直线AB上,若∠BOC=60°,则∠AOC的大小是( )
 如图,点O在直线AB上,若∠BOC=60°,则∠AOC的大小是( )
如图,点O在直线AB上,若∠BOC=60°,则∠AOC的大小是( )| A. | 60° | B. | 90° | C. | 120° | D. | 150° |
 如图,矩形ABCD中,点E、F分别在边CD、AB上,且DE=BF.
如图,矩形ABCD中,点E、F分别在边CD、AB上,且DE=BF.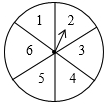 如图,一个质地均匀的转盘被平均分成6等份,分别标有数字1,2,3,4,5,6,当它停止时,指针指向的数字即为转出的数字(若指针指在分界线上,则重新转动转盘).小颖与小亮进行转盘游戏,规则是:若转出的数是3的倍数则小颖获胜,若不是3的倍数则小亮获胜.
如图,一个质地均匀的转盘被平均分成6等份,分别标有数字1,2,3,4,5,6,当它停止时,指针指向的数字即为转出的数字(若指针指在分界线上,则重新转动转盘).小颖与小亮进行转盘游戏,规则是:若转出的数是3的倍数则小颖获胜,若不是3的倍数则小亮获胜.