题目内容
3.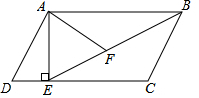 如图,在?ABCD中 过点A作AE⊥DC,垂足为E,连接BE,F为BE上一点,且∠AFE=∠D.
如图,在?ABCD中 过点A作AE⊥DC,垂足为E,连接BE,F为BE上一点,且∠AFE=∠D.(1)求证:△ABF∽△BEC;
(2)若AD=5,AB=8,sinD=$\frac{4}{5}$,求AF的长.
分析 (1)由平行四边形的性质得出AB∥CD,AD∥BC,AD=BC,得出∠D+∠C=180°,∠ABF=∠BEC,证出∠C=∠AFB,即可得出结论;
(2)由勾股定理求出BE,由三角函数求出AE,再由相似三角形的性质求出AF的长.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,AD=BC,
∴∠D+∠C=180°,∠ABF=∠BEC,
∵∠AFB+∠AFE=180°,
∴∠C=∠AFB,
∴△ABF∽△BEC;
(2)解:∵AE⊥DC,AB∥DC,
∴∠AED=∠BAE=90°,
在Rt△ABE中,根据勾股定理得:BE=$\sqrt{A{E}^{2}+A{B}^{2}}$=$\sqrt{{4}^{2}+{8}^{2}}$=4$\sqrt{5}$,
在Rt△ADE中,AE=AD•sinD=5×$\frac{4}{5}$=4,
∵BC=AD=5,
由(1)得:△ABF∽△BEC,
∴$\frac{AF}{BC}=\frac{AB}{BE}$,即$\frac{AF}{5}=\frac{8}{4\sqrt{5}}$,
解得:AF=2$\sqrt{5}$.
点评 此题考查了相似三角形的判定与性质,以及平行四边形的性质,熟练掌握相似三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
13.“约在江苏,共筑梦想”,为了解某校1000名学生在2017年5月20日“江苏发展大会”期间对会议的关注方式,某班兴趣小组随机抽取了部分学生进行问卷调查,某校抽取学生“江苏发展大会”期间对会议的关注方式的统计表并将问卷调查的结果绘制成如下不完整的统计表:
(1)本次问卷调查抽取的学生共有50人,其中通过电视关注会议的学生有8人;
(2)从上表的“频数”、“百分比”两列数据中选择一列,用适当的统计图表示;
(3)根据抽样的结果,估计该校学生通过报纸关注会议的约有多少人?
| 方式 | 频数 | 百分比 |
| 网络 | 23 | 46% |
| 电视 | ||
| 报纸 | 8% | |
| 其他 | 15 | |
| 合计 | 100% |
(2)从上表的“频数”、“百分比”两列数据中选择一列,用适当的统计图表示;
(3)根据抽样的结果,估计该校学生通过报纸关注会议的约有多少人?
14.通过估算,估计$\sqrt{19}$的值应在( )
| A. | 2~3之间 | B. | 3~4之间 | C. | 4~5之间 | D. | 5~6之间 |
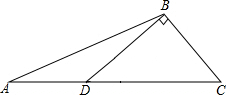 如图,在钝角△ABC中,过钝角顶点B作BD⊥BC交AC于点D.请用尺规作图法在BC边上求作一点P,使得点P到AC的距离等于BP的长.(保留作图痕迹,不写作法)
如图,在钝角△ABC中,过钝角顶点B作BD⊥BC交AC于点D.请用尺规作图法在BC边上求作一点P,使得点P到AC的距离等于BP的长.(保留作图痕迹,不写作法) 如图,点E在直线DF上,点B在直线AC上,若∠1=∠2,∠3=∠4,则∠A=∠F,请说明理由.
如图,点E在直线DF上,点B在直线AC上,若∠1=∠2,∠3=∠4,则∠A=∠F,请说明理由. 如图,矩形ABCD中,点E、F分别在边CD、AB上,且DE=BF.
如图,矩形ABCD中,点E、F分别在边CD、AB上,且DE=BF.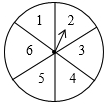 如图,一个质地均匀的转盘被平均分成6等份,分别标有数字1,2,3,4,5,6,当它停止时,指针指向的数字即为转出的数字(若指针指在分界线上,则重新转动转盘).小颖与小亮进行转盘游戏,规则是:若转出的数是3的倍数则小颖获胜,若不是3的倍数则小亮获胜.
如图,一个质地均匀的转盘被平均分成6等份,分别标有数字1,2,3,4,5,6,当它停止时,指针指向的数字即为转出的数字(若指针指在分界线上,则重新转动转盘).小颖与小亮进行转盘游戏,规则是:若转出的数是3的倍数则小颖获胜,若不是3的倍数则小亮获胜.