题目内容
4.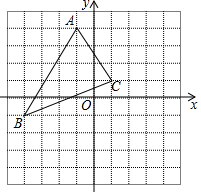 如图,在平面直角坐标系中,A(-1,4),B(-4,-1),C(1,1).
如图,在平面直角坐标系中,A(-1,4),B(-4,-1),C(1,1).(1)三角形ABC中任意一点P(x,y)经平移后对应点为P′(x+4,y+1),将三角形ABC作同样的平移得到三角形A′B′C′,画出三角形A′B′C′,并写出点A′,B′,C′的坐标:A′(3,5),B′(0,0),C′(5,2).
(2)求三角形ABC的面积.
分析 (1)根据题意可知把△ABC先向右平移4个单位,再向上平移1个单位即可得到△A′B′C′,画出△A′B′C′,并写出各点坐标即可;
(2)利用正方形的面积减去三个顶点上三角形的面积即可.
解答 解:(1)∵△ABC中任意一点P(x,y)经平移后对应点为P′(x+4,y+1),
∴把△ABC先向右平移4个单位,再向上平移1个单位即可得到△A′B′C′,
∴△A′B′C′如图所示,
由图可知A′(3,5),B′(0,0),C′(5,2).
故答案为:(3,5),(0,0),(5,2);
(2)S△ABC=5×5-$\frac{1}{2}$×5×3-$\frac{1}{2}$×2×3-$\frac{1}{2}$×2×5=25-$\frac{15}{2}$-3-5=$\frac{19}{2}$.
点评 本题考查的是作图-平移变换,熟知图形平移不变性的性质是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.通过估算,估计$\sqrt{19}$的值应在( )
| A. | 2~3之间 | B. | 3~4之间 | C. | 4~5之间 | D. | 5~6之间 |
16.在实数$\frac{\sqrt{2}}{2}$,-$\root{3}{8}$,3.14,0中,无理数是( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | -$\root{3}{8}$ | C. | 3.14 | D. | 0 |
14.要反映一个家庭在教育方面支出占总收入的比,宜采用( )
| A. | 条形统计图 | B. | 扇形统计图 | C. | 折线统计图 | D. | 频数分布直方图 |
 如图,点E在直线DF上,点B在直线AC上,若∠1=∠2,∠3=∠4,则∠A=∠F,请说明理由.
如图,点E在直线DF上,点B在直线AC上,若∠1=∠2,∠3=∠4,则∠A=∠F,请说明理由. 如图,矩形ABCD中,点E、F分别在边CD、AB上,且DE=BF.
如图,矩形ABCD中,点E、F分别在边CD、AB上,且DE=BF.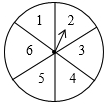 如图,一个质地均匀的转盘被平均分成6等份,分别标有数字1,2,3,4,5,6,当它停止时,指针指向的数字即为转出的数字(若指针指在分界线上,则重新转动转盘).小颖与小亮进行转盘游戏,规则是:若转出的数是3的倍数则小颖获胜,若不是3的倍数则小亮获胜.
如图,一个质地均匀的转盘被平均分成6等份,分别标有数字1,2,3,4,5,6,当它停止时,指针指向的数字即为转出的数字(若指针指在分界线上,则重新转动转盘).小颖与小亮进行转盘游戏,规则是:若转出的数是3的倍数则小颖获胜,若不是3的倍数则小亮获胜.