题目内容
9.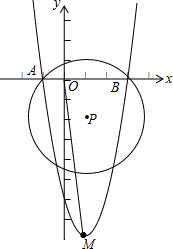 如图.以点P(1,-2)为圆心,$2\sqrt{2}$为半径的⊙P交x轴于点A,B,抛物线y=ax2+bx+c经过点A,B和点M(1,-8).
如图.以点P(1,-2)为圆心,$2\sqrt{2}$为半径的⊙P交x轴于点A,B,抛物线y=ax2+bx+c经过点A,B和点M(1,-8).(1)求点A,B坐标;
(2)求抛物线的解析式;
(3)抛物线上是否存在点Q,使PQ和OM互相平分?如果存在,求出点Q坐标;不存在请简要说明理由.
分析 (1)过P作PM⊥x轴于M,连接PA、PB,根据勾股定理求出AM、BM即可;
(2)把A、B、M的坐标代入抛物线得出方程组,求出方程组的解即可;
(3)求出抛物线和y轴的交点,即可得出此点符合条件.
解答 解: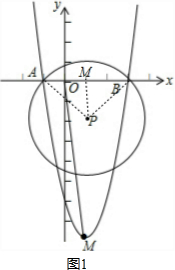
(1)过P作PM⊥x轴于M,连接PA、PB,如图1,
∵以点P(1,-2)为圆心,$2\sqrt{2}$为半径的⊙P交x轴于点A,B,
∴PA=PB,PM=2,OM=1,PA=PB=2$\sqrt{2}$,
由勾股定理得:AM=BM=2,
∴A(-1,0),B(3,0);
(2)把A、B、M的坐标代入y=ax2+bx+c得:M(1,-8)
$\left\{\begin{array}{l}{a-b+c=0}\\{9a+3b+c=0}\\{a+b+c=-8}\end{array}\right.$,
解得:a=a2,b=-4,c=-6,
所以抛物线的解析式是y=2x2-4x-6;
(3)如图2,y=2x2-4x-6,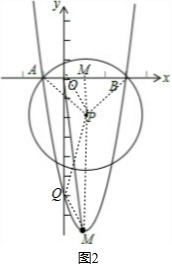
当x=0时,y=-6,
即Q点的坐标是(0,-6),
连接PQ、OP、QM,
此时QMPO是平行四边形,
所以OM和PQ互相平分,
即抛物线上存在点Q,使PQ和OM互相平分,此时点Q坐标是(0,-6).
点评 本题考查了勾股定理,用待定系数法求二次函数的解析式,平行四边形的判定的应用,能综合性运用性质进行计算是解此题的关键,难度偏大.

练习册系列答案
相关题目
20.根据加法的交换律,由式子-a+b-c可得( )
| A. | b-a+c | B. | -b+a+c | C. | b-a-c | D. | -b+a-c |
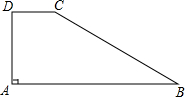 如图所示,四边形ABCD中,AD⊥DC,AD=8,DC=6,CB=24,AB=26,求四边形ABCD的面积.
如图所示,四边形ABCD中,AD⊥DC,AD=8,DC=6,CB=24,AB=26,求四边形ABCD的面积.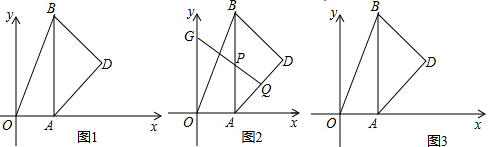


 如图,三个全等的小矩形沿“横一竖一横“排列在一个大的边长分别为12.34,23.45的矩形中,则图中一个小矩形的周长等于23.86.
如图,三个全等的小矩形沿“横一竖一横“排列在一个大的边长分别为12.34,23.45的矩形中,则图中一个小矩形的周长等于23.86.