题目内容
2.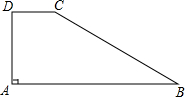 如图所示,四边形ABCD中,AD⊥DC,AD=8,DC=6,CB=24,AB=26,求四边形ABCD的面积.
如图所示,四边形ABCD中,AD⊥DC,AD=8,DC=6,CB=24,AB=26,求四边形ABCD的面积.
分析 连接AC,先根据勾股定理求出AC的长,在根据勾股定理的逆定理推出△ACB也是直角三角形,然后将两个直角三角形的面积相加即可.
解答 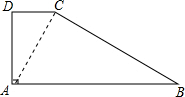 解:连接AC,
解:连接AC,
∵在Rt△ADC中,∠D=90°,CD=6,AD=8,
∴AC=$\sqrt{A{D}^{2}+D{C}^{2}}$=10,
又因为在△ACB中,AB2=AC2+BC2,
∴△ACB也是直角三角形.
∴四边形ABCD的面积等于S△ADC+S△ACB,
即$\frac{1}{2}$AD•DC+$\frac{1}{2}$AC•BC=$\frac{1}{2}$×6×8+×10×24=144.
答:图中四边形ABCD的面积为144.
点评 此题主要考查学生对勾股定理和勾股定理的逆定理的理解和掌握,解答此题的关键是利用勾股定理的逆定理推出△ACB也是直角三角形,然后即可得出答案了.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
13.当a,b取任意有理数时,代数式(1)2(a+1)2+(2a-1)2;(2)a2-7a+12;(3)(4-3a)2+(b-4)2;(4)|3a-2b-4|+3a2-12a+13中,其值恒为正的有( )个.
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
17.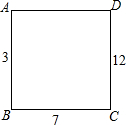 如图,在正方形ABCD的每个顶点上写一个数,把这个正方形每条边的两端点上的数加起来,将和写在这条边上,已知AB上的数是3,BC上的数是7,CD上的数是12,则AD上的数是( )
如图,在正方形ABCD的每个顶点上写一个数,把这个正方形每条边的两端点上的数加起来,将和写在这条边上,已知AB上的数是3,BC上的数是7,CD上的数是12,则AD上的数是( )
 如图,在正方形ABCD的每个顶点上写一个数,把这个正方形每条边的两端点上的数加起来,将和写在这条边上,已知AB上的数是3,BC上的数是7,CD上的数是12,则AD上的数是( )
如图,在正方形ABCD的每个顶点上写一个数,把这个正方形每条边的两端点上的数加起来,将和写在这条边上,已知AB上的数是3,BC上的数是7,CD上的数是12,则AD上的数是( )| A. | 2 | B. | 7 | C. | 8 | D. | 15 |
7.某商场试销一种商品,成本为每件200元,规定试销期间销售单价不低于成本单价,且获利不得高于50%,一段时间后,发现销售量y(件)与销售单价x(元)之间的函数关系如表:
(1)请根据表格中所给数据,求出y关于x的函数关系式;
(2)设商场所获利润为w元,将商品销售单价定为多少时,才能使所获利润最大?最大利润是多少?
| 销售单价x(元) | … | 230 | 235 | 240 | 245 | … |
| 销售量y(件) | … | 440 | 430 | 420 | 410 | … |
(2)设商场所获利润为w元,将商品销售单价定为多少时,才能使所获利润最大?最大利润是多少?
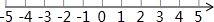




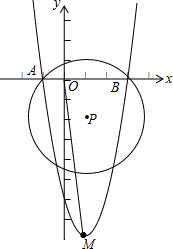 如图.以点P(1,-2)为圆心,$2\sqrt{2}$为半径的⊙P交x轴于点A,B,抛物线y=ax2+bx+c经过点A,B和点M(1,-8).
如图.以点P(1,-2)为圆心,$2\sqrt{2}$为半径的⊙P交x轴于点A,B,抛物线y=ax2+bx+c经过点A,B和点M(1,-8).