题目内容
4.如图1,在平面直角坐标系中,AB⊥x轴正半轴于点A,连接OB,B(2,8),AD是∠BAO外角的角平分线,过点B作BD⊥AD于点D.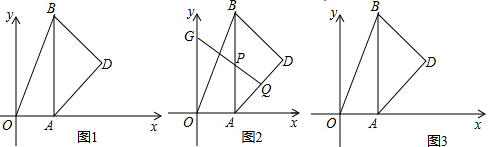
(1)求点D的坐标;
(2)如图2,动点P,从B点出发,沿BA以2个单位的速度向A运动,PQ∥BD交AD于点Q,交y轴于点G,设四边形OAQG的面积为S,运动时间为t,请用t表示S的关系式;
(3)在(2)的条件下,当t为何值时,Rt△OAP的两直角边的比为2:1;并求此时直线PQ与x轴交点M的坐标.
分析 (1)先证得△ABD是等腰直角三角形,根据等腰三角形的性质证得DE=AE=$\frac{1}{2}$AB,即可求得D的坐标;
(2)根据题意求得OG=10-2t,PA=8-2t,然后根据S=S梯形APGO+S△PAQ,即可求得用t表示S的关系式;
(3)根据题意求得P(2,4)或(2,1),然后根据待定系数法求得PQ的解析式,即可求得直线PQ与x轴交点M的坐标.
解答 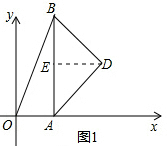 解:(1)如图1,∵AB⊥x轴正半轴于点A,AD是∠BAO外角的角平分线,
解:(1)如图1,∵AB⊥x轴正半轴于点A,AD是∠BAO外角的角平分线,
∴∠DAB=45°,
∵BD⊥AD,
∴∠DBA=45°,
∴△ABD是等腰直角三角形,
作DE⊥AB于D,
∴DE=AE=$\frac{1}{2}$AB,
∵B(2,8),
∴AE=DE=4,
∴D(6,4);
(2)如图2,∵B(2,8),D(6,4),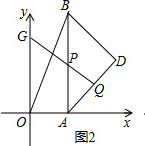
∴直线BD的解析式为y=-x+10,
∴直线BD与y轴的交点F的坐标为(0,10),
∵AB∥y轴,BD∥PQ,
∴四边形DQGF是平行四边形,
∴FG=PB=2t,
∴OG=10-2t,PA=8-2t,
∵BD∥PQ,
∴PQ⊥AD,
∴△APQ是等腰直角三角形,
∴PQ=AQ=$\frac{\sqrt{2}}{2}$AP=$\frac{\sqrt{2}}{2}$(8-2t),
∴S=S梯形APGO+S△PAQ=$\frac{1}{2}$(8-2t+10-2t)×2+$\frac{1}{2}$×$\frac{\sqrt{2}}{2}$(8-2t)×$\frac{\sqrt{2}}{2}$(8-2t),
=t2-12t+34,
即S=t2-12t+34,(0≤t≤4);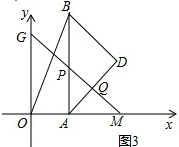
(3)如图3,∵Rt△OAP的两直角边的比为2:1,OA=2,
∴AP=4或1,
当AP=4时,则P(2,4),
∵BD∥PQ,直线BD的解析式为y=-x+10,
∴设直线PQ的解析式为y=-x+n,
把P(2,4)代入得,4=-2+n,交点n=6,
∴直线PQ的解析式为y=-x+6,
∴M(6,0);
当AP=1时,则P(2,1),
同理,即可求得M(3,0),
∴P的坐标为(6,0)或(3,0).
点评 本题考查了等腰直角三角形的判定和性质,待定系数法求一次函数的解析式,根据题意求得线段OG、PA、PQ、AQ的长是解题的关键.

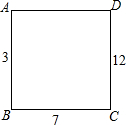 如图,在正方形ABCD的每个顶点上写一个数,把这个正方形每条边的两端点上的数加起来,将和写在这条边上,已知AB上的数是3,BC上的数是7,CD上的数是12,则AD上的数是( )
如图,在正方形ABCD的每个顶点上写一个数,把这个正方形每条边的两端点上的数加起来,将和写在这条边上,已知AB上的数是3,BC上的数是7,CD上的数是12,则AD上的数是( )| A. | 2 | B. | 7 | C. | 8 | D. | 15 |
| A. | 同为正数 | B. | 同为负数 | ||
| C. | 一个为零一个为负数 | D. | 至少一个为负数,且负数绝对值大 |
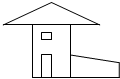 如图所示的是一座房子的平面图,组成这幅图的几何图形有( )
如图所示的是一座房子的平面图,组成这幅图的几何图形有( )| A. | 三角形、长方形 | B. | 三角形、正方形、长方形 | ||
| C. | 三角形、正方形、长方形、梯形 | D. | 正方形、长方形、梯形 |
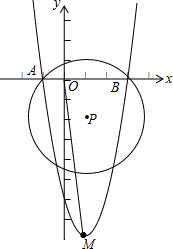 如图.以点P(1,-2)为圆心,$2\sqrt{2}$为半径的⊙P交x轴于点A,B,抛物线y=ax2+bx+c经过点A,B和点M(1,-8).
如图.以点P(1,-2)为圆心,$2\sqrt{2}$为半径的⊙P交x轴于点A,B,抛物线y=ax2+bx+c经过点A,B和点M(1,-8).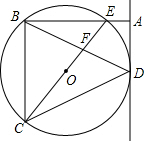 如图,⊙O为△BCD的外接圆,CE为⊙O的直径,过D作⊙O的切线交BE的延长线于A,且AD∥BC,BD交CE于F.
如图,⊙O为△BCD的外接圆,CE为⊙O的直径,过D作⊙O的切线交BE的延长线于A,且AD∥BC,BD交CE于F.