��Ŀ����
1��������ABCD�ı߳�Ϊ3����E��F�ֱ�������DC��DA���˶�����DE=DF������BF����EH��BF����ֱ���ڵ�H������CH����1����ͼ1������E��DC���е㣬CH��AB֮���������ϵ��CH=AB��
��2����ͼ2������E��DC�����Ҳ���DC���е�ʱ����1���еĽ����Ƿ����������������֤��������������˵�����ɣ�
��3����ͼ3������E��F�ֱ�������DC��DA���˶�ʱ������DH������D��ֱ��DH�Ĵ��ߣ���ֱ��BF�ڵ�K������CK����ֱ��д���߶�CK�������ֵ��
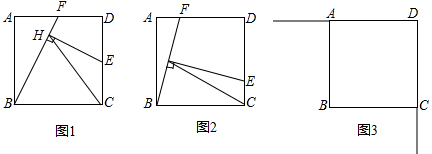
���� ��1�����ȸ���ȫ���������ж��ķ������жϳ���ABF�ա�CBE�������жϳ���1=��2��Ȼ�����EH��BF����BCE=90�㣬�ɵ�C��H���㶼����BEΪֱ����Բ�ϣ��жϳ���4=��HBC�������жϳ�CH=BC��������AB=BC���жϳ�CH=AB���ɣ�
��2�����ȸ���ȫ���������ж��ķ������жϳ���ABF�ա�CBE�������жϳ���1=��2��Ȼ�����EH��BF����BCE=90�㣬�ɵ�C��H���㶼����BEΪֱ����Բ�ϣ��жϳ���4=��HBC�������жϳ�CH=BC��������AB=BC���жϳ�CH=AB���ɣ�
��3�����ȸ������������ߵĹ�ϵ���ɵ�CK��AC+AK���ݴ��жϳ���C��A��K���㹲��ʱ��CK�ij����Ȼ�����ȫ���������ж��ķ������жϳ���DFK�ա�DEH�������жϳ�DK=DH���ٸ���ȫ���������ж��ķ������жϳ���DAK�ա�DCH�������жϳ�AK=CH=AB��������CK=AC+AK=AC+AB������߶�CK�������ֵ�Ƕ��ټ��ɣ�
��� �⣺��1����ͼ1������BE��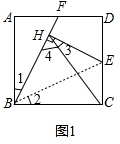 ��
��
��������ABCD��
AB=BC=CD=AD����A=��BCD=��ABC=90�㣬
�ߵ�E��DC���е㣬DE=DF��
���F��AD���е㣬
��AF=CE��
�ڡ�ABF�͡�CBE�У�
$\left\{\begin{array}{l}AB=CB\\��A=��BCE\\ AF=CE\end{array}\right.$
���ABF�ա�CBE��
���1=��2��
��EH��BF����BCE=90�㣬
��C��H���㶼����BEΪֱ����Բ�ϣ�
���3=��2��
���1=��3��
�ߡ�3+��4=90�㣬��1+��HBC=90�㣬
���4=��HBC��
��CH=BC��
�֡�AB=BC��
��CH=AB��
�ʴ�Ϊ��CH=AB��
��2������E��DC�����Ҳ���DC���е�ʱ����1���еĽ���CH=AB��Ȼ������
��ͼ2������BE��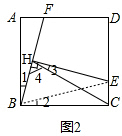 ��
��
��������ABCD��
AB=BC=CD=AD����A=��BCD=��ABC=90�㣬
��AD=CD��DE=DF��
��AF=CE��
�ڡ�ABF�͡�CBE�У�
$\left\{\begin{array}{l}AB=CB\\��A=��BCE\\ AF=CE\end{array}\right.$
���ABF�ա�CBE��
���1=��2��
��EH��BF����BCE=90�㣬
��C��H���㶼����BEΪֱ����Բ�ϣ�
���3=��2��
���1=��3��
�ߡ�3+��4=90�㣬��1+��HBC=90�㣬
���4=��HBC��
��CH=BC��
�֡�AB=BC��
��CH=AB��
��3����ͼ3��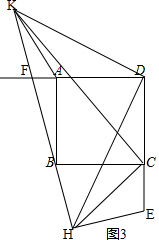 ��
��
��CK��AC+AK��
�൱C��A��K���㹲��ʱ��CK�ij����
�ߡ�KDF+��ADH=90�㣬��HDE+��ADH=90�㣬
���KDF=��HDE��
�ߡ�DEH+��DFH=360��-��ADC-��EHF=360��-90��-90��=180�㣬
��DFK+��DFH=180�㣬
���DFK=��DEH��
�ڡ�DFK�͡�DEH�У�
$\left\{\begin{array}{l}{��KDF=��HDE}\\{DF=DE}\\{��DFK=��DEH}\end{array}\right.$
���DFK�ա�DEH��
��DK=DH��
�ڡ�DAK�͡�DCH�У�
$\left\{\begin{array}{l}{DA=DC}\\{��KDA=��HDC}\\{DK=DH}\end{array}\right.$
���DAK�ա�DCH��
��AK=CH
�֡�CH=AB��
��AK=CH=AB��
��AB=3��
��AK=3��AC=3$\sqrt{2}$��
��CK=AC+AK=AC+AB=$3\sqrt{2}+3$��
���߶�CK�������ֵ��$3\sqrt{2}+3$��
���� ��1��������Ҫ�������ı����ۺ��⣬�����˷����������������������ν�Ϸ�����Ӧ�ã�Ҫ�������գ�
��2�����������ȫ�������ε��ж������ʵ�Ӧ�ã��Լ������ε����ʺ�Ӧ�ã�Ҫ�������գ�
��3������������߶γ��ȵ����ֵ����Ҫ�������գ�

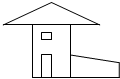 ��ͼ��ʾ����һ�����ӵ�ƽ��ͼ��������ͼ�ļ���ͼ���У�������
��ͼ��ʾ����һ�����ӵ�ƽ��ͼ��������ͼ�ļ���ͼ���У�������| A�� | �����Ρ������� | B�� | �����Ρ������Ρ������� | ||
| C�� | ���������������������� | D�� | ���������������� |
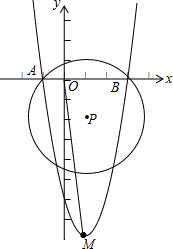 ��ͼ���Ե�P��1��-2��ΪԲ�ģ�$2\sqrt{2}$Ϊ�뾶�ġ�P��x���ڵ�A��B��������y=ax2+bx+c������A��B�͵�M��1��-8����
��ͼ���Ե�P��1��-2��ΪԲ�ģ�$2\sqrt{2}$Ϊ�뾶�ġ�P��x���ڵ�A��B��������y=ax2+bx+c������A��B�͵�M��1��-8����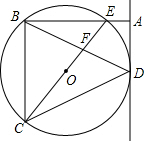 ��ͼ����OΪ��BCD�����Բ��CEΪ��O��ֱ������D����O�����߽�BE���ӳ�����A����AD��BC��BD��CE��F��
��ͼ����OΪ��BCD�����Բ��CEΪ��O��ֱ������D����O�����߽�BE���ӳ�����A����AD��BC��BD��CE��F��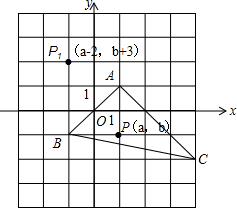 ��ͼ��ʾ����ABC�У�����һ��P��a��b����ƽ�ƺ��Ӧ��P1��a-2��b+3��������ABC��ͬ����ƽ�Ƶõ���A1B1C1������A1B1C1����д��A1��B1��C1�����ꣻ���A1B1C1�����
��ͼ��ʾ����ABC�У�����һ��P��a��b����ƽ�ƺ��Ӧ��P1��a-2��b+3��������ABC��ͬ����ƽ�Ƶõ���A1B1C1������A1B1C1����д��A1��B1��C1�����ꣻ���A1B1C1�����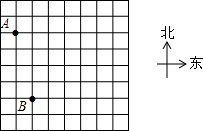 ��һ������Ӫ��У���ʦ��һ���ж��ƻ�����û���κα�ǵĵ�C����ֻ���ߴ��������־��A��B������ֱ�Ϊ��-3��1������-2��-3�����Լ���C������Ϊ��3��2������λ��km����
��һ������Ӫ��У���ʦ��һ���ж��ƻ�����û���κα�ǵĵ�C����ֻ���ߴ��������־��A��B������ֱ�Ϊ��-3��1������-2��-3�����Լ���C������Ϊ��3��2������λ��km����