题目内容
19.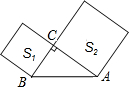 如图,以Rt△ABC的两直角边为边向外作正方形,其面积分别为S1、S2,若S1=9,S2=16,则斜边AB的长是( )
如图,以Rt△ABC的两直角边为边向外作正方形,其面积分别为S1、S2,若S1=9,S2=16,则斜边AB的长是( )| A. | 3 | B. | 4 | C. | 5 | D. | 25 |
分析 根据正方形的面积公式求出AC、BC,根据勾股定理计算即可.
解答 解:∵S1=9,S2=16,
∴BC=3,AC=4,
∴AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=5,
故选:C.
点评 本题考查的是勾股定理的应用,直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
11.适合下列条件的△ABC,直角三角形的个数为( )
①a=1,b=2,c=$\sqrt{3}$;
②∠A:∠B:∠C=3:4:5;
③a2-b2=c2;
④∠A+∠B=∠C;
⑤a=$\frac{1}{3}$,b=$\frac{1}{4}$,c=$\frac{1}{5}$.
①a=1,b=2,c=$\sqrt{3}$;
②∠A:∠B:∠C=3:4:5;
③a2-b2=c2;
④∠A+∠B=∠C;
⑤a=$\frac{1}{3}$,b=$\frac{1}{4}$,c=$\frac{1}{5}$.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
12.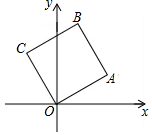 如图,点A在第一象限内,其坐标为(2,1),以OA为边在x轴上方作正方形OABC,则正方形OABC的顶点C的坐标是( )
如图,点A在第一象限内,其坐标为(2,1),以OA为边在x轴上方作正方形OABC,则正方形OABC的顶点C的坐标是( )
 如图,点A在第一象限内,其坐标为(2,1),以OA为边在x轴上方作正方形OABC,则正方形OABC的顶点C的坐标是( )
如图,点A在第一象限内,其坐标为(2,1),以OA为边在x轴上方作正方形OABC,则正方形OABC的顶点C的坐标是( )| A. | (-2,1) | B. | (1,3) | C. | (1,2) | D. | (-1.2) |
7.为了解某种车的耗油量,专业技术人员对这种车在高速公路上做了耗油试验,测得的数据如下表:
(1)根据上表的数据,写出Q与t的关系式Q=100-6t;
(2)汽车行驶5小时后,油箱中的剩余油量是70L;
(3)若汽车油箱中剩余油量为52升,则汽车行使了8小时;
(4)贮满100升汽油的汽车,理论上最多能行驶$\frac{50}{3}$小时.
| 汽车行驶时间t(时) | 0 | 1 | 2 | 3 | … |
| 油箱剩余油量Q(升) | 100 | 94 | 88 | 82 | … |
(2)汽车行驶5小时后,油箱中的剩余油量是70L;
(3)若汽车油箱中剩余油量为52升,则汽车行使了8小时;
(4)贮满100升汽油的汽车,理论上最多能行驶$\frac{50}{3}$小时.



 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别是A(-3,2),B(-1,4),C(0,2)
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别是A(-3,2),B(-1,4),C(0,2)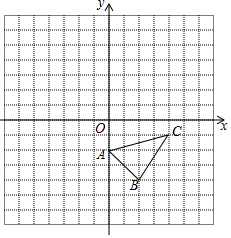 已知:如图,已知△ABC.
已知:如图,已知△ABC.