题目内容
11.适合下列条件的△ABC,直角三角形的个数为( )①a=1,b=2,c=$\sqrt{3}$;
②∠A:∠B:∠C=3:4:5;
③a2-b2=c2;
④∠A+∠B=∠C;
⑤a=$\frac{1}{3}$,b=$\frac{1}{4}$,c=$\frac{1}{5}$.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 根据勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形;三角形内角和为180°进行分析即可.
解答 解:①12+($\sqrt{3}$)2=22,是直角三角形;
②∵∠A:∠B:∠C=3:4:5,∴∠C=180°×$\frac{5}{3+4+5}$=75°,不能构成直角三角形;
③∵a2-b2=c2,∴a2=b2+c2,是直角三角形;
④∵∠A+∠B=∠C,∴∠C=90°,是直角三角形;
⑤∵($\frac{1}{4}$)2+($\frac{1}{5}$)2≠($\frac{1}{3}$)2,不能构成直角三角形;
故能构成直角三角形的个数为3个.
故选:B.
点评 此题主要考查了直角三角形的判定,关键是掌握勾股定理的逆定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.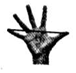 如图,大拇指与小拇指尽量张开时,两指间的距离称为指距.某项研究表明,一般情况下人的身高(ycm)是指距(xcm)的一次函数.下表是测得的一组数据:
如图,大拇指与小拇指尽量张开时,两指间的距离称为指距.某项研究表明,一般情况下人的身高(ycm)是指距(xcm)的一次函数.下表是测得的一组数据:
(1)求y与x的函数关系式;(不要求写出x的取值范围)
(2)如果李华的指距为22cm,那么他的身高的为多少?
 如图,大拇指与小拇指尽量张开时,两指间的距离称为指距.某项研究表明,一般情况下人的身高(ycm)是指距(xcm)的一次函数.下表是测得的一组数据:
如图,大拇指与小拇指尽量张开时,两指间的距离称为指距.某项研究表明,一般情况下人的身高(ycm)是指距(xcm)的一次函数.下表是测得的一组数据:| 指距x(cm) | 19 | 20 | 21 |
| 身高y(cm) | 151 | 160 | 169 |
(2)如果李华的指距为22cm,那么他的身高的为多少?





 有意义,那么x的取值范围是 ( )
有意义,那么x的取值范围是 ( ) B. x>-
B. x>- C. x
C. x D. x
D. x
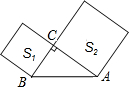 如图,以Rt△ABC的两直角边为边向外作正方形,其面积分别为S1、S2,若S1=9,S2=16,则斜边AB的长是( )
如图,以Rt△ABC的两直角边为边向外作正方形,其面积分别为S1、S2,若S1=9,S2=16,则斜边AB的长是( )