题目内容
当b分别为何值时,一次函数y=2x+b的图象与反比例函数y=-
的图象:
①有一个公共点;
②有两个公共点;
③无公共点.
| 2 |
| x |
①有一个公共点;
②有两个公共点;
③无公共点.
考点:反比例函数与一次函数的交点问题
专题:
分析:把y=2x+b代入y=-
,整理即可得到一个关于x的一元二次方程,求得方程的判别式△,
①有一个公共点,则△=0,求得k的值;
②有两个公共点,则△=0,求得k的值;
③无公共点,则△<0,求得k的值.
| 2 |
| x |
①有一个公共点,则△=0,求得k的值;
②有两个公共点,则△=0,求得k的值;
③无公共点,则△<0,求得k的值.
解答:解:把y=2x+b代入y=-
得:2x+b=-
,
则2x2+bx+2=0,
△=b2-16.
①b2-16=0,
解得:b=4或-4;
②b2-16>0,
解得:b>4或b<-4;
③b2-16<0,
解得:-4<b<4.
| 2 |
| x |
| 2 |
| x |
则2x2+bx+2=0,
△=b2-16.
①b2-16=0,
解得:b=4或-4;
②b2-16>0,
解得:b>4或b<-4;
③b2-16<0,
解得:-4<b<4.
点评:本题考查了一次函数与反比例函数的交点的个数的判定,利用判别式△判断.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
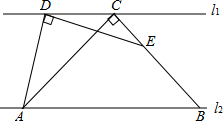 已知,如图,l1∥l2,AC=BC,∠ADE=90°,∠ACB=90°,求证:AD=DE.
已知,如图,l1∥l2,AC=BC,∠ADE=90°,∠ACB=90°,求证:AD=DE.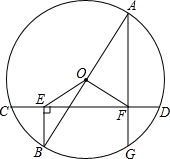 已知,AB为圆O的直径,CD是弦,BE⊥CD于E,AF⊥CD于F,连接OE,OF,求证:
已知,AB为圆O的直径,CD是弦,BE⊥CD于E,AF⊥CD于F,连接OE,OF,求证: