题目内容
8. 如图,在△ABC中,∠B=48°,三角形的外角∠DAC和∠ACF的平分线交于点E,∠AEC等于( )
如图,在△ABC中,∠B=48°,三角形的外角∠DAC和∠ACF的平分线交于点E,∠AEC等于( )| A. | 56° | B. | 66° | C. | 76° | D. | 无法确定 |
分析 根据三角形内角和定理、角平分线的定义以及三角形外角定理求得$\frac{1}{2}$∠DAC+$\frac{1}{2}$∠ACF=$\frac{1}{2}$(∠B+∠B+∠1+∠2)=114°;最后在△AEC中利用三角形内角和定理可以求得∠AEC的度数.
解答 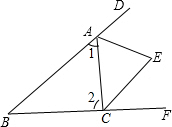 解:∵三角形的外角∠DAC和∠ACF的平分线交于点E,
解:∵三角形的外角∠DAC和∠ACF的平分线交于点E,
∴∠EAC=$\frac{1}{2}$∠DAC,∠ECA=$\frac{1}{2}$∠ACF,
∵∠DAC=∠B+∠2,∠ACF=∠B+∠1
∴$\frac{1}{2}$∠DAC+$\frac{1}{2}$∠ACF=$\frac{1}{2}$(∠B+∠2)+$\frac{1}{2}$(∠B+∠1)=$\frac{1}{2}$(∠B+∠B+∠1+∠2),
∵∠B=48°(已知),∠B+∠1+∠2=180°(三角形内角和定理),
∴$\frac{1}{2}$∠DAC+$\frac{1}{2}$∠ACF=114°
∴∠AEC=180°-($\frac{1}{2}$∠DAC+$\frac{1}{2}$∠ACF)=66°.
故选B.
点评 本题考查了三角形内角和定理、三角形外角性质.解题时注意挖掘出隐含在题干中已知条件“三角形内角和是180°”.

练习册系列答案
相关题目
 如图,点C、D是线段AB上的两点,若AC=4,CD=8,DB=3,
如图,点C、D是线段AB上的两点,若AC=4,CD=8,DB=3,