题目内容
17.矩形ABCD中,相邻两边的长分别为4cm、$4\sqrt{3}$cm,则两条对角线夹角是( )| A. | 90° | B. | 30°或150° | C. | 45°或135° | D. | 60°或120° |
分析 由矩形的性质、勾股定理和已知条件可得出△AOB是等边三角形,得出∠AOB=60°,∠AOD=120°即可.
解答 解:如图所示: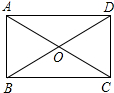
∵四边形ABCD是矩形,
∴∠ABC=90°,OA=OC=$\frac{1}{2}$AC,OB=OD=$\frac{1}{2}$BD,AC=BD,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=8,OA=OB,
∴OA=OB=4,
∴OA=OB=AB,
∴△AOB是等边三角形,
∴∠AOB=60°,
∴∠AOD=120°,
即两条对角线夹角是60°或120°.
故选:D.
点评 本题主要考查了矩形的性质、等边三角形的判定与性质、勾股定理;熟练掌握矩形的性质,证出△AOB是等边三角形是解决问题的关键.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
12.⊙O的半径为5cm,弦AB∥CD,且AB=8cm,CD=6cm,则AB与CD之间的距离为( )
| A. | 1cm | B. | 7cm | C. | 3cm或4cm | D. | 1cm或7cm |
2.计算$\sqrt{\frac{1}{x}}$÷$\sqrt{x}$×$\sqrt{x^2}$的值为( )
| A. | 1 | B. | x | C. | $\frac{1}{x}$ | D. | x2 |
7.某公司以每吨200元的价格购进某种矿石原料300吨,用于生产甲、乙两种产品,生产1吨甲产品或1吨乙产品所需该矿石和煤原料的吨数如下表:
煤的价格为400元/吨,生产1吨甲产品除原料费用外,还需其它费用400元,甲产品每吨售价4600元;生产1吨乙产品除原料费用外,还需其它费用500元,乙产品每吨售价5500元,现将该矿石原料全部用完.设生产甲产品x吨.
(1)用含x的式子表示乙产品的吨数;
(2)用含x的式子表示公司生产两种产品的总利润.
| 产品/资源 | 甲 | 乙 |
| 矿石(t) | 10 | 4 |
| 煤(t) | 4 | 8 |
(1)用含x的式子表示乙产品的吨数;
(2)用含x的式子表示公司生产两种产品的总利润.
 二次函数y=(k+2)x2的图象如图所示,则k的取值范围是k>-2.
二次函数y=(k+2)x2的图象如图所示,则k的取值范围是k>-2.