题目内容
当正整数m为何值时，关于x的方程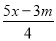
＝
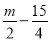的解是非正数？
m＝1或2或3.
【解析】【试题分析】求出不等式＝的解集为 ，再根据方程的解为非正数，得不等式m－3≤0，解不等式得：m≤3，因为m为正整数，m＝1或2或3.
【试题解析】
＝
去分母得：
移项得：
系数化为1 得：
又 m－3≤0，
∴m≤3，
∵m为正整数，
∴m＝1或2或3.
故答案为：m＝1或2或3.
孟建平小学滚动测试系列答案下列说法正确的是( )
A. 为了审核书稿中的错别字,选择抽样调查
B. 为了了解春节联欢晚会的收视率,选择全面调查
C. “射击运动员射击一次,命中靶心”是随机事件
D. “经过有交通信号灯的路口,遇到红灯”是必然事件
C
【解析】试题分析：为了审核书稿中的错别字，应选择全面调查，A错误；
为了了解春节联欢晚会的收视率，选择抽样调查，B错误；
“射击运动员射击一次，命中靶心”是随机事件，C正确；
“经过由交通信号灯的路口，遇到红灯”是随机事件，D错误．
故选C．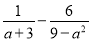 
________.
【解析】试题分析：
＝
＝
＝
＝．
故答案为： ． 为了落实党中央提出的“惠民政策”，我市今年计划开发建设A、B两种户型的“廉租房”共40套．投入资金不超过200万元，又不低于198万元．开发建设办公室预算：一套A型“廉租房”的造价为5.2万元，一套B型“廉租房”的造价为4.8万元．
（1）请问有几种开发建设方案？
（2）哪种建设方案投入资金最少？最少资金是多少万元？
（3）在（2）的方案下，为了让更多的人享受到“惠民”政策，开发建设办公室决定通过缩小“廉租房”的面积来降低造价、节省资金．每套A户型“廉租房”的造价降低0.7万元，每套B户型“廉租房”的造价降低0.3万元，将节省下来的资金全部用于再次开发建设缩小面积后的“廉租房”，如果同时建设A、B两种户型，请你直接写出再次开发建设的方案．
（1）共有6种方案
（2）当x=15时，W最小， 198万元
（3）再建设方案：①A型住房1套，B型住房3套；
②A型住房2套，B型住房2套；
③A型住房3套，B型住房1套．
【解析】
【解析】
（1）设建设A型x套，则B型（40-x）套，
根据题意得，，
解不等式①得，x≥15，
解不等式②得，x≤20，
所以，不等式组的解集是15≤... 一个矩形，两边长分别为xcm和10cm，如果它的周长小于80cm，面积大于100cm2，则x的取值范围是__．
10＜x＜30
【解析】【解析】
矩形的周长是2（x+10）cm，面积是10xcm2．根据题意，得：
，
解不等式：2（x+10）＜80，
解得：x＜30，
解不等式：10x＞100，
解得：x＞10，
所以x的取值范围是：10＜x＜30．
故答案为：10＜x＜30． 如果不等式ax＋4＜0的解集在数轴上表示如图，那么a的值为____.
-2
【解析】解不等式ax＋4＜0得， 由数轴上可得：不等式的解集为： ,则 解得： .
故答案为 如图，点B、D、E、C在一条直线上，△ABD≌△ACE，AB和AC，AD和AE是对应边，除△ABD≌△ACE外，图中还有其他全等三角形吗？若有，请写出来，并证明你的结论。
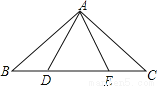
有，△ABE≌△ACD
【解析】试题分析：
由△ABD≌△ACE可得：AB=AC，BD=CE，∠B=∠C，从而易得BE=CD，这样由“SAS”即可证得△ABE和△ACD.
试题解析：
有，△ABE≌△ACD；理由如下：
∵△ABD≌△ACE，
∴AB=AC，BD=CE，∠B=∠C，
∴BE=CD，
在△ABE和△ACD中，
，
∴△ABE... 某次知识竞赛共有20道题，每一题答对得10分，答错或不答都扣5分，娜娜得分要超过90分，设她答对了n道题，则根据题意可列不等式 ．
10n﹣5（20﹣n）＞90
【解析】根据答对题的得分：10n；答错题的得分：﹣5（20﹣n），得出不等关系：得分要超过90分．
【解析】
根据题意，得10n﹣5（20﹣n）＞90．
故答案为：10n﹣5（20﹣n）＞90． 如图，在?ABCD中，E是BC的中点，连接AE并延长交DC的延长线于点F．
（1）求证：AB=CF；
（2）连接DE，若AD=2AB，求证：DE⊥AF．
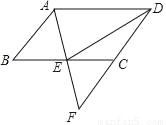
（1）证明见解析（2）证明见解析
【解析】试题分析：（1）由在?ABCD中，E是BC的中点，利用ASA，即可判定△ABE≌△FCE，继而证得结论；（2）由AD=2AB，AB=FC=CD，可得AD=DF，又由△ABE≌△FCE，可得AE=EF，然后利用三线合一，证得结论．
试题解析：（1）∵四边形ABCD是平行四边形， ∴AB∥DF， ∴∠ABE=∠FCE， ∵E为BC中点， ∴BE=C...