��Ŀ����
Ϊ����ʵ����������ġ��������ߡ������н���ƻ���������A��B���ֻ��͵ġ����ⷿ����40�ף�Ͷ���ʽ���200��Ԫ���ֲ�����198��Ԫ����������칫��Ԥ�㣺һ��A�͡����ⷿ�������Ϊ5.2��Ԫ��һ��B�͡����ⷿ�������Ϊ4.8��Ԫ��
��1�������м��ֿ������跽����
��2�����ֽ��跽��Ͷ���ʽ����٣������ʽ��Ƕ�����Ԫ��
��3���ڣ�2���ķ����£�Ϊ���ø���������ܵ����������ߣ���������칫�Ҿ���ͨ����С�����ⷿ���������������ۡ���ʡ�ʽ�ÿ��A���͡����ⷿ������۽���0.7��Ԫ��ÿ��B���͡����ⷿ������۽���0.3��Ԫ������ʡ�������ʽ�ȫ�������ٴο���������С�����ġ����ⷿ�������ͬʱ����A��B���ֻ��ͣ�����ֱ��д���ٴο�������ķ�����
 ��1������6�ַ���
��2����x=15ʱ��W��С�� 198��Ԫ
��3���ٽ��跽������A��ס��1�ף�B��ס��3�ף�
��A��ס��2�ף�B��ס��2�ף�
��A��ס��3�ף�B��ס��1�ף�
��������
��������
��1���轨��A��x�ף���B�ͣ�40-x���ף�
����������
�ⲻ��ʽ�ٵã�x��15��
�ⲻ��ʽ�ڵã�x��20��
���ԣ�����ʽ��Ľ⼯��15��...
��1������6�ַ���
��2����x=15ʱ��W��С�� 198��Ԫ
��3���ٽ��跽������A��ס��1�ף�B��ס��3�ף�
��A��ס��2�ף�B��ס��2�ף�
��A��ס��3�ף�B��ס��1�ף�
��������
��������
��1���轨��A��x�ף���B�ͣ�40-x���ף�
����������
�ⲻ��ʽ�ٵã�x��15��
�ⲻ��ʽ�ڵã�x��20��
���ԣ�����ʽ��Ľ⼯��15��...
��ͼ�����ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O���������������ж��ı���ABCDΪƽ���ı��ε��ǣ� ��
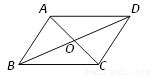
A. AB��CD��AD��BC B. OA=OC��OB=OD
C. AD=BC��AB��CD D. AB=CD��AD=BC
 D
��������������Ա߷ֱ�ƽ�е��ı�����ƽ���ı��ο�֪A��ȷ;
�ɶԽ�����ƽ�ֵ��ı�����ƽ���ı��ο�֪B��ȷ;
��һ��Ա�ƽ������ȵ��ı�����ƽ���ı��ο�֪C����ȷ;
������Ա߷ֱ���ȵ��ı�����ƽ���ı��ο�֪D��ȷ;
��ѡC
D
��������������Ա߷ֱ�ƽ�е��ı�����ƽ���ı��ο�֪A��ȷ;
�ɶԽ�����ƽ�ֵ��ı�����ƽ���ı��ο�֪B��ȷ;
��һ��Ա�ƽ������ȵ��ı�����ƽ���ı��ο�֪C����ȷ;
������Ա߷ֱ���ȵ��ı�����ƽ���ı��ο�֪D��ȷ;
��ѡC ��֪��ʽ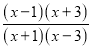 �����壬��x��ȡֵΪ�� ��
�����壬��x��ȡֵΪ�� ��
A. x�٣�1 B. x��3 C. x�٣�1��x��3 D. x�٣�1��x��3
 C
�������������������ʽ�ķ�ĸ����Ϊ0�����ԣ� �����x�٣�1��x��3.
��ѡC.
C
�������������������ʽ�ķ�ĸ����Ϊ0�����ԣ� �����x�٣�1��x��3.
��ѡC. ���㣺 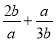 ��________
��________
 �����������������ԭʽ��
����
�ʴ�Ϊ�� ��
�����������������ԭʽ��
����
�ʴ�Ϊ�� �� ��ʽ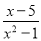 ��
�� �Ĺ���ĸ�ǣ� ��
�Ĺ���ĸ�ǣ� ��
A.  B.
B.  C.
C. 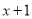 D.
D. 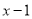
 A
�����������������x2��1��(x��1)(x��1)��
���Է�ʽ��Ĺ���ĸ��(x��1)(x��1)��
��x2��1��
��ѡA��
A
�����������������x2��1��(x��1)(x��1)��
���Է�ʽ��Ĺ���ĸ��(x��1)(x��1)��
��x2��1��
��ѡA�� ����•�ġ�����ڣ�����ί��֯������ѧ����Աȥ��ɽֲ����ijУ���꼶��3������֧���쵽һ�����磬��ÿ��ֲ4��������ʣ37�ã���ÿ��ֲ6�����������һ������ֲ��������3�ã��������繲��__�ã�
 121
����������������
������ί��֯������ѧ����Ա��x�ˣ��������У�4x+37���ã�������ã�
1�ܣ�4x+37����6��x��1����3
ȥ���ŵã�1�ܩ�2x+43��3��
����ã���42�ܩ�2x����40��
��ã�20��x��21��
��xȡ����������x=21��
��x=21ʱ��4x+37=4��21+37=121����������4��21+37=121�ã�
�ʴ�...
121
����������������
������ί��֯������ѧ����Ա��x�ˣ��������У�4x+37���ã�������ã�
1�ܣ�4x+37����6��x��1����3
ȥ���ŵã�1�ܩ�2x+43��3��
����ã���42�ܩ�2x����40��
��ã�20��x��21��
��xȡ����������x=21��
��x=21ʱ��4x+37=4��21+37=121����������4��21+37=121�ã�
�ʴ�... ��������mΪ��ֵʱ������x�ķ���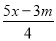 ��
��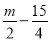 �Ľ��Ƿ�������
�Ľ��Ƿ�������
 m��1��2��3.
��������������������������ʽ���Ľ⼯Ϊ ���ٸ��ݷ��̵Ľ�Ϊ���������ò���ʽm��3��0���ⲻ��ʽ�ã�m��3����ΪmΪ��������m��1��2��3.
�����������
��
ȥ��ĸ�ã�
����ã�
ϵ����Ϊ1 �ã�
�� m��3��0��
��m��3��
��m��������
��m��1��2��3.
�ʴ�Ϊ��m��1��2��3.
m��1��2��3.
��������������������������ʽ���Ľ⼯Ϊ ���ٸ��ݷ��̵Ľ�Ϊ���������ò���ʽm��3��0���ⲻ��ʽ�ã�m��3����ΪmΪ��������m��1��2��3.
�����������
��
ȥ��ĸ�ã�
����ã�
ϵ����Ϊ1 �ã�
�� m��3��0��
��m��3��
��m��������
��m��1��2��3.
�ʴ�Ϊ��m��1��2��3. ��ͼ�����������ܱ�֤��ABC�ա�ADC���ǣ���AB=AD��BC=DC���ڡ�1=��3����4=��2���ۡ�1=��2����4=��3���ܡ�1=��2��AB=AD���ݡ�1=��2��BC=DC����������
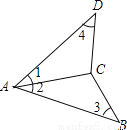
A. �٢ڢۢܢ� B. �٢ڢۢ� C. �٢ۢ� D. �٢ۢܢ�
 C
�����������ڡ�ABC�͡�ADC�У�AC=AC��
�൱������������AB=AD��BC=DCʱ�����ɡ�SSS���õ���ABC�ա�ADC��
�������������ڡ�1=��3����4=��2ʱ�����ܵõ���ABC�ա�ADC��
�������������ۡ�1=��2����4=��3ʱ�����ɡ�AAS���õ���ABC�ա�ADC��
�������������ܡ�1=��2��AB=ADʱ�����ɡ�SAS���õ���ABC�ա�ADC��
...
C
�����������ڡ�ABC�͡�ADC�У�AC=AC��
�൱������������AB=AD��BC=DCʱ�����ɡ�SSS���õ���ABC�ա�ADC��
�������������ڡ�1=��3����4=��2ʱ�����ܵõ���ABC�ա�ADC��
�������������ۡ�1=��2����4=��3ʱ�����ɡ�AAS���õ���ABC�ա�ADC��
�������������ܡ�1=��2��AB=ADʱ�����ɡ�SAS���õ���ABC�ա�ADC��
... Ҫʹ����ʽ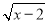 ������,��x��ȡֵ��Χ��( )
������,��x��ȡֵ��Χ��( )
A.x��2 B.x��-2 C.x��-2 D.x��2
 A��
��������
����������������⣬��
x-2��0��
��ã�x��2��
��ѡA��
A��
��������
����������������⣬��
x-2��0��
��ã�x��2��
��ѡA�� 
