题目内容
17．
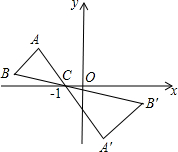如图，△ABC中，A，B两个顶点在x轴的上方，点C的坐标是（-1，0）．以点C为位似中心，在x轴的下作△ABC的位似图形△A′B′C，并把△ABC的边长放大到原来的2倍．设点A′的对应点A的纵坐标是1.5，则点A'的纵坐标是（ ）| A． | 3 | B． | -3 | C． | -4 | D． | 4 |
分析 根据位似变换的性质得出△ABC的边长放大到原来的2倍，进而得出点A'的纵坐标．
解答 解：∵点C的坐标是（-1，0）．以点C为位似中心，在x轴的下方作△ABC的位似图形△A′B′C，
并把△ABC的边长放大到原来的2倍．
点A′的对应点A的纵坐标是1.5，
则点A'的纵坐标是：-3．
故选：B．
点评 此题主要考查了位似变换的性质，根据已知得出纵坐标的绝对值是2倍关系是解决问题的关键．
练习册系列答案
阅读快车系列答案
相关题目
7．
如图，已知△ABC为等边三角形，若沿图中虚线剪去∠B，则∠1+∠2等于（ ）
如图，已知△ABC为等边三角形，若沿图中虚线剪去∠B，则∠1+∠2等于（ ）| A． | 120° | B． | 135° | C． | 240° | D． | 315° |
8．定义：平面内的直线l1与l2相交于点O，对于该平面内任意一点M，点M到直线l1、l2的距离分别为a、b，则称有序非负实数对（a，b）是点M的“距离坐标”，根据上述定义，距离坐标为（2，1）的点的个数有（ ）
| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
5．-3，0，-1，2四个数中，绝对值最大的数是（ ）
| A． | -3 | B． | 0 | C． | 2 | D． | -1 |
6．已知⊙O的半径为2，则⊙O的内接正三角形的面积为（ ）
| A． | $\frac{3}{2}\sqrt{3}$ | B． | 3$\sqrt{3}$ | C． | 6$\sqrt{3}$ | D． | 12$\sqrt{3}$ |