题目内容
12.某村为解决村民出行难的问题,村委会决定将一条长为1200m的村级公路硬化,并将该项工程承包给甲、乙两工程队来施工.并将该项工程承包给甲、乙两工程队来施工,若甲、乙两队做需12天完成此项工程;若甲队先做了8天后,剩下的由乙队单独做还需18天才能完工.(1)问甲、乙两队单独完成此项工程各需多少天?
(2)又已知甲队每施工一天需要费用2万元,乙队每施工一天需要费用1万元,要使完成该工程所需费用不超过35万元,则乙工程队至少要施工多少天?
分析 (1)设甲单独做需要用x天,乙单独做需要y天,利用工作效率得出等式组成方程组求出即可;
(2)首先求出两队的工效,进而表示出两队需要的费用得出不等式求出即可.
解答 解:(1)设甲单独做需要用x天,乙单独做需要y天,根据题意可得:
$\left\{\begin{array}{l}{\frac{1}{x}+\frac{1}{y}=\frac{1}{12}}\\{\frac{8}{x}+\frac{18}{y}=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=20}\\{y=30}\end{array}\right.$.
答:甲单独做需要用20天,乙单独做需要30天;
(2)甲的工效:1200÷20=60,乙的工效:1200÷30=40,
∵2×20=40>35,
∴设乙需要做a天,由题意可得:
2×$\frac{1200-40a}{60}$+a≤35,
解得:a≥15.
答:乙工程队至少要施工15天.
点评 此题主要考查了一元一次不等式的应用以及分式方程的应用,根据题意得出两队的工效,进而得出等量关系是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.已知多项式x2+3x=3,可求得另一个多项式3x2+9x-4的值为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
7.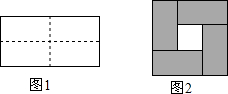 图(1)是一个长为2m,宽为2n(m>n)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是( )
图(1)是一个长为2m,宽为2n(m>n)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是( )
 图(1)是一个长为2m,宽为2n(m>n)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是( )
图(1)是一个长为2m,宽为2n(m>n)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是( )| A. | (m+n)2=m2+2mn+n2 | B. | (m+n)2-4mn=(m-n)2 | C. | (m+n)2-(m-n)2=4mn | D. | m2-n2=(m+n)(m-n) |
17.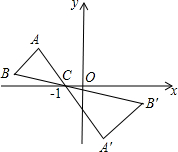 如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x轴的下作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点A′的对应点A的纵坐标是1.5,则点A'的纵坐标是( )
如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x轴的下作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点A′的对应点A的纵坐标是1.5,则点A'的纵坐标是( )
 如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x轴的下作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点A′的对应点A的纵坐标是1.5,则点A'的纵坐标是( )
如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x轴的下作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点A′的对应点A的纵坐标是1.5,则点A'的纵坐标是( )| A. | 3 | B. | -3 | C. | -4 | D. | 4 |
4.下列运算错误的是( )
| A. | -(a-2b)=-a+2b | B. | a2•a3=a5 | C. | (a-2)2=a2+4 | D. | 3a-2a=a |
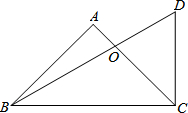 一次综合实践活动中,小明同学拿到一只含45°角的三角板和一只含30°角的三角板,如图放置恰好有一边重合,则S△ODC:S△OAB的值为$\frac{3+\sqrt{3}}{3}$.
一次综合实践活动中,小明同学拿到一只含45°角的三角板和一只含30°角的三角板,如图放置恰好有一边重合,则S△ODC:S△OAB的值为$\frac{3+\sqrt{3}}{3}$.