题目内容
 如图,设C、D是以O为圆心、AB为直径的半圆上的任意两点,过点B作⊙O的切线交直线CD交于P,直线PO与直线CA、AD分别交于点E、F.证明:OE=OF.
如图,设C、D是以O为圆心、AB为直径的半圆上的任意两点,过点B作⊙O的切线交直线CD交于P,直线PO与直线CA、AD分别交于点E、F.证明:OE=OF.考点:四点共圆
专题:证明题
分析:过O作OM⊥CD于M,连结BC、BM、BD、BE,根据垂径定理由OM⊥CD得CM=DM,且∠OMD=90°,根据切线的性质得∠OBP=90°,可判断O、B、P、M四点共圆,根据圆周角定理得∠BMP=∠BOP,而∠BOP=∠AOE,所以∠BMP=∠AOP,根据圆内接四边形的性质得∠MDB=∠EAO,于是可判断△OAE∽△MDB,得到
=
,利用DM=
CD,OA=
AB得到
=
,加上∠CDB=∠BAE,根据相似的判定方法得到△BAE∽△CDB,则∠EBA=∠BCD,而根据圆周角定理能得到∠BCD=∠BAD,所以∠EBA=∠BAD,则根据平行线的判定得到AD∥BE,再根据三角形相似的判定方法得到△OBE∽△OAF,利用相似比即可得到OE=OF.
| AE |
| BD |
| AO |
| DM |
| 1 |
| 2 |
| 1 |
| 2 |
| AE |
| BD |
| AB |
| CD |
解答: 证明:过O作OM⊥CD于M,连结BC、BM、BD、BE,如图,
证明:过O作OM⊥CD于M,连结BC、BM、BD、BE,如图,
∵OM⊥CD,
∴CM=DM,∠OMD=90°,
∵PB为⊙O的切线,
∴∠OBP=90°,
∴∠OMP+∠OBP=180°,
∴O、B、P、M四点共圆,
∴∠BMP=∠BOP,
∵∠BOP=∠AOE,
∴∠BMP=∠AOP,
∵∠MDB=∠EAO,
∴△OAE∽△MDB,
∴
=
,
∵DM=
CD,OA=
AB,
∴
=
,
而∠CDB=∠BAE,
∴△BAE∽△CDB,
∴∠EBA=∠BCD,
∵∠BCD=∠BAD,
∴∠EBA=∠BAD,
∴AD∥BE,
∴△OBE∽△OAF,
∴
=
,
而OB=OA,
∴OE=OF.
 证明:过O作OM⊥CD于M,连结BC、BM、BD、BE,如图,
证明:过O作OM⊥CD于M,连结BC、BM、BD、BE,如图,∵OM⊥CD,
∴CM=DM,∠OMD=90°,
∵PB为⊙O的切线,
∴∠OBP=90°,
∴∠OMP+∠OBP=180°,
∴O、B、P、M四点共圆,
∴∠BMP=∠BOP,
∵∠BOP=∠AOE,
∴∠BMP=∠AOP,
∵∠MDB=∠EAO,
∴△OAE∽△MDB,
∴
| AE |
| BD |
| AO |
| DM |
∵DM=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| AE |
| BD |
| AB |
| CD |
而∠CDB=∠BAE,
∴△BAE∽△CDB,
∴∠EBA=∠BCD,
∵∠BCD=∠BAD,
∴∠EBA=∠BAD,
∴AD∥BE,
∴△OBE∽△OAF,
∴
| OE |
| OF |
| OB |
| OA |
而OB=OA,
∴OE=OF.
点评:本题考查了四点共圆:若四点连成四边形的对角互补或一个外角等于内对角,那么这四点共圆;圆内接四边形的对角互补,一个外角等于它的内对角;也考查了垂径定理、圆周角定理、切线的性质和相似三角形的判定与性质.

练习册系列答案
相关题目
在频数分布直方图中,各个小长方形的高( )
| A、与频数成正比 |
| B、与频数成反比 |
| C、与频数不成正比也不成反比 |
| D、与频数无关 |
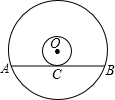 如图所示是一张电脑光盘的表面,两个圆的圆心是点O,大圆的弦AB所在直线是小圆的切线,弦AB=4
如图所示是一张电脑光盘的表面,两个圆的圆心是点O,大圆的弦AB所在直线是小圆的切线,弦AB=4 如图,在Rt△ABC中,∠A=90°,∠C=30°,将△ABC沿BD折叠,使点A落在BC边上的E点处,求证:BD=CD.
如图,在Rt△ABC中,∠A=90°,∠C=30°,将△ABC沿BD折叠,使点A落在BC边上的E点处,求证:BD=CD. 如图,已知⊙O1、⊙O2外切于点P,它们的半径分别为4和1,直线l与⊙O1、⊙O2分别相切于点A、B,求直线O1O2与直线l所成锐角∠T的正弦值.
如图,已知⊙O1、⊙O2外切于点P,它们的半径分别为4和1,直线l与⊙O1、⊙O2分别相切于点A、B,求直线O1O2与直线l所成锐角∠T的正弦值.