题目内容

阅读下列解题过程：
1
2
+1
=
2
-1
(
2
+1)(
2
-1)
=
2
-1
1
3
+
2
=
3
-
2
(
3
+
2
)(
3
-
2
)
=
3
-
2

1
4
+
3
=
4
-
3
(
4
+
3
)(
4
-
3
)
=
4
-
3
；
则：
（1）
1
11
+
10
=
 
；
1
2014
+
2013
=
 
；
（2）观察上面的解题过程，请直接写出式子
1
n
+
n+1
=
 
．
考点：分母有理化
专题：规律型
分析：（1）仿照例题中的计算方法计算即可得到结果；
（2）以此类推得到一般性规律，写出即可．
解答：解：（1）
1
11
+
10
=
11
-
10
(
11
+
10
)(
11
-
10
)
=
11
-
10
；
1
2014
+
2013
=
2014
-
2013
(
2014
+
2013
)(
2014
-
2013
)
2014
-
2013
；
（2）
1
n
+
n+1
=
n+1
-
n
． 
故答案为：（1）
11
-
10
；
2014
-
2013
；（2）
n+1
-
n
点评：此题考查了分母有理化，二次根式有理化主要利用了平方差公式，所以一般二次根式的有理化因式是符合平方差公式的特点的式子．即一项符号和绝对值相同，另一项符号相反绝对值相同．
练习册系列答案
相关题目
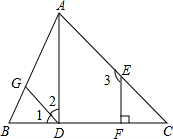等腰三角形一腰上的中线把周长分为15和12两部分，求该三角形各边的长．
如图，已知EF⊥BC，∠1=∠C，∠2+∠3=180°．试说明直线AD与BC垂直（请在下面的解答过程的空格内填空或在括号内填写理由）
理由：
∵∠1=∠C，（已知）
∴GD∥AC，（
 
）
∴∠2=
 
（两直线平行，内错角相等）
又∵∠2+∠3=180°（已知）
∴∠3+
 
=180°（等量代换）
∴AD∥EF（
 
）
∴∠ADC=∠EFC（
 
）
∵EF⊥BC，（已知）
∴∠EFC=90°，∴∠ADC=90°．
如图，在直角标系xOy中，点A的坐标为（1，0），点B、C的坐标分别为（-1，0）、（0，b），且0＜b＜3，直线l是过点B、C的直线，当点C在线段OC上移动时，过点A作AD⊥l交l于点D．
（1）求点D、O之间的距离；
（2）如果S△BDA：S△BOC=a，试求a与b的函数关系式及a的取值范围；
（3）当∠ADO的正切值为
1
2
时，求直线l的解析式，并求此时△ABD与△BOC重叠部分的面积．
某校为了了解学生的身体发育情况，在7-9年级学生中抽取部分学生的身高进行抽样统计，制作了统计图和统计表，但不够完整，图表如下：
组别 身高（cm） 频数 频率
     1 130.5～140.5  3  0.05
     2  140.5～150.5  m  0.15
     3  150.5～160.5
     4  160.5～170.5
    5  170.5～180.5  n
 合计

请根据上面图表解答下列问题
①填空m=
 
，n=
 
；    
②补全频数分布直方图；
③“中位数”可能在哪一组（不要求说明理由）
如图，△ABC，△CEF均为等腰直角三角形，∠ABC=∠CEF=90°，C、B、E在同一直线上，连接AF，M是AF的中点，连接MB、ME．延长BM交EF于点D．
求证：MB=MD=ME．
如图，在11×11的正方形网格中，每个小正方形的边长都为1，网格中有一个格点△ABC（即三角形的顶点都在格点上）．
（1）在图中作出△ABC关于直线l对称的△A1B1C1；（要求A与A1，B与B1，C与C1相对应）
（2）作出△ABC绕点C顺时针方向旋转90°后得到的△A2B2C；
（3）在（2）的条件下求出线段CB旋转到CB2所扫过的面积．（结果保留π）
如图，点D为△ABC的边AC的中点，AE∥BC，连接ED并延长交BC的延长线于F，交AB于H，若AH：HB=1：3，BC=8，则AE的长为
 
．
观察下列等式：
①
1
2
-1
=
2
+1；②
1
3
-
2
=
3
+
2
；③
1
2-
3
=2+
3
，
根据以上的规律则第n个等式
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网