Question

8．己知反比例函数y=$\frac{k}{x}$经过点E（3，4），在反比例函数图象上找一点P，满足∠POE=45°，则P点坐标为（2$\sqrt{21}$，$\frac{6\sqrt{21}}{21}$）．

Answer 1

分析 过点E作EA⊥x轴于点A，过点P作PB⊥x轴于点B，由点E在反比例函数图象上得出k=12，设点P的坐标为（n，$\frac{12}{n}$），通过分割图形求出△OEP的面积，再根据面积公式表示出△OEP的面积，由此即可得出关于n的一元四次方程，结合函数图象解方程即可得出结论．

解答 解：过点E作EA⊥x轴于点A，过点P作PB⊥x轴于点B，如图所示．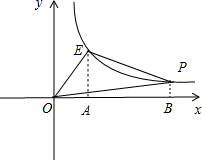

∵点E（3，4）在函数y=$\frac{k}{x}$的图象上，
∴k=3×4=12，
∴设点P的坐标为（n，$\frac{12}{n}$），则点A（3，0），点B（n，0），
S_{四边形OBPE}=S_△OAE+S_梯形PBAE=$\frac{1}{2}$|k|+$\frac{1}{2}$（PB+EA）•AB=6+$\frac{1}{2}$（$\frac{12}{n}$+4）（n-3）=2n-$\frac{18}{n}$+6．
S_△OEP=S_{四边形OBPE}-S_△OBP=2n-$\frac{18}{n}$+6-$\frac{1}{2}$|k|=2n-$\frac{18}{n}$．
由两点间的距离公式可知：
OE=$\sqrt{{3}^{2}+{4}^{2}}$=5，OP=$\sqrt{{n}^{2}+（\frac{12}{n}）^{2}}$，
S_△OEP=$\frac{1}{2}$OE•OP•sin∠EOP=$\frac{5\sqrt{2}}{4}$$\sqrt{{n}^{2}+（\frac{12}{n}）^{2}}$=2n-$\frac{18}{n}$，
即7n⁴-576n²-1008=0，
解得：n²=84或n²=-84（舍去），
∴n₁=2$\sqrt{21}$，n₂=-2$\sqrt{21}$（舍去）．
∴点P的坐标为（2$\sqrt{21}$，$\frac{6\sqrt{21}}{21}$）．
故答案为：（2$\sqrt{21}$，$\frac{6\sqrt{21}}{21}$）．

点评 本题考查了反比例函数图象上点的坐标特征以及解一元高次方程，解题的关键是得出关于n的一元四次方程．本题属于中档题，难道不大，但较繁琐，解决该题型题目时，根据三角形面积的不同求法得出关于n的一元高次方程是关键．