题目内容
14.梯形ABCD中,AD∥BC,若要使顺次连接ABCD各边中点所得的四边形为矩形,只需( )| A. | AB=DC | B. | AC=BD | C. | AB=DC且AC=BD | D. | AC⊥BD |
分析 根据所有中点四边形均是平行四边形,然后添加使得平行四边形为矩形的条件即可.
解答 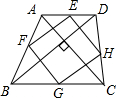 解:如图,当AC⊥BD时,四边形EFGH为矩形;
解:如图,当AC⊥BD时,四边形EFGH为矩形;
E、F、G、H分别为各边的中点,连接点E、F、G、H.
∵E、F、G、H分别为各边的中点,
∴EF∥AC,GH∥AC,EH∥BD,FG∥BD,(三角形的中位线平行于第三边)
∴四边形EFGH是平行四边形,(两组对边分别平行的四边形是平行四边形)
∵AC⊥BD,EF∥AC,EH∥BD,
∴∠EMO=∠ENO=90°,
∴四边形EMON是矩形(有三个角是直角的四边形是矩形),
∴∠MEN=90°,
∴四边形EFGH是矩形(有一个角是直角的平行四边形是矩形).
故选D.
点评 此题主要考腰梯形的性质、平行四边形判定、三角形的中位线定理,关键是掌握三角形的中位线平行于第三边且等于第三边的一半.

练习册系列答案
相关题目
2.-2-2的倒数等于( )
| A. | -4 | B. | 4 | C. | -$\frac{1}{4}$ | D. | $\frac{1}{4}$ |
9.“每天锻炼一小时,健康生活一辈子”.新泰市自开展“阳光体育运动”以来,学校师生的锻炼意识都增强了,某校有学生3000人,为了解学生每天的锻炼时间,学校体育组随机调查了部分学生,统计结果如表所示.
该校每天锻炼时间达到1小时及以上的约有300人.
| 时间段 | 29分钟及以下 | 30-39分钟 | 40-49分钟 | 50-59分钟 | 1小时及以上 |
| 频数/人 | 108 | 20 | |||
| 频率 | 0.54 | 0.12 | 0.09 |
6. 如图,正六边形ABCDEF内接于⊙O,已知弦心距OM=3,则此正六边形的边长为( )
如图,正六边形ABCDEF内接于⊙O,已知弦心距OM=3,则此正六边形的边长为( )
 如图,正六边形ABCDEF内接于⊙O,已知弦心距OM=3,则此正六边形的边长为( )
如图,正六边形ABCDEF内接于⊙O,已知弦心距OM=3,则此正六边形的边长为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |