题目内容
9.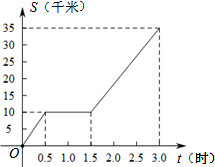 一辆自行车在公路上行驶,中途发生了故障,停下修理一段时间后继续前进.已知行驶路程S(千米)与所用时间t(时)的函数关系的图象如图所示,那么自行车发生故障后继续前进的速度为( )
一辆自行车在公路上行驶,中途发生了故障,停下修理一段时间后继续前进.已知行驶路程S(千米)与所用时间t(时)的函数关系的图象如图所示,那么自行车发生故障后继续前进的速度为( )| A. | 20千米/时 | B. | $\frac{35}{3}$千米/时 | C. | 10千米/时 | D. | $\frac{50}{3}$千米/时 |
分析 根据图象得出自行车发生故障后经过点(1.5,10)和(3.0,35),再得出其路程和时间,得出速度即可.
解答 解:由图象可得:自行车发生故障后的图象经过点(1.5,10)和(3.0,35),
可得路程为35-10=25,时间为3.0-1.5=1.5,
可得速度=$\frac{25}{1.5}=\frac{50}{3}$千米/小时,
故选D.
点评 此题考查图象问题,关键是根据图象得出解析式图象经过两点,得出路程和时间进行解答.

练习册系列答案
相关题目
1.在某校科技节“知识竞赛”中共进行四次比赛,甲、乙两个参赛同学,四次比赛成绩情况下表所示:
设两同学得分的平均数依次为$\overline{{x}_{甲}}$,$\overline{{x}_{乙}}$,得分的方差依次为$S_甲^2$,$S_乙^2$,则下列关系中完全正确的是( )
| 次数 | 第一次 | 第二次 | 第三次 | 第四次 |
| 甲 | 9.7 | 10 | 10 | 8.4 |
| 乙 | 9.2 | 10 | 9.7 | 9.2 |
| A. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,S甲2>S乙2 | B. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,$S_甲^2<S_乙^2$ | ||
| C. | $\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$,$S_甲^2>S_乙^2$ | D. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,$S_甲^2<S_乙^2$ |
18.在平行四边形、正方形、正五边形、正六边形四个图形中是中心对称图形的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
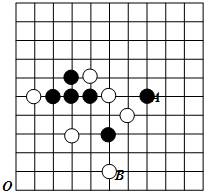 五子棋是一种两人对弈的棋类游戏,规则是:在正方形棋盘中,由黑方先行,白方后行,轮流弈子,下在棋盘横线与竖线的交叉点上,直到某一方首先在任一方向(横向、竖向或者是斜着的方向)上连成五子者为胜.如图,这一部分棋盘是两个五子棋爱好者的对弈图.观察棋盘,以点O为原点,在棋盘上建立平面直角坐标系,将每个棋子看成一个点,若黑子A的坐标为(7,5),则白子B的坐标为(5,1);为了不让白方获胜,此时黑方应该下在坐标为(3,7)或(7,3)的位置处.
五子棋是一种两人对弈的棋类游戏,规则是:在正方形棋盘中,由黑方先行,白方后行,轮流弈子,下在棋盘横线与竖线的交叉点上,直到某一方首先在任一方向(横向、竖向或者是斜着的方向)上连成五子者为胜.如图,这一部分棋盘是两个五子棋爱好者的对弈图.观察棋盘,以点O为原点,在棋盘上建立平面直角坐标系,将每个棋子看成一个点,若黑子A的坐标为(7,5),则白子B的坐标为(5,1);为了不让白方获胜,此时黑方应该下在坐标为(3,7)或(7,3)的位置处.