题目内容
4. 如图,在菱形ABCD中,AB=5,∠BCD=120°,则菱形的面积为$\frac{25\sqrt{3}}{2}$.
如图,在菱形ABCD中,AB=5,∠BCD=120°,则菱形的面积为$\frac{25\sqrt{3}}{2}$.
分析 作AE⊥BC于E,在Rt△ABE中,由三角函数求出AE,即可得出菱形的面积.
解答 解:作AE⊥BC于E,如图所示:
∵四边形ABCD是菱形,∠BCD=120°,
∴AB=BC=5,∠ABC=60°,
∴AE=AB•sin60°=5×$\frac{\sqrt{3}}{2}$=$\frac{5\sqrt{3}}{2}$,
∴菱形ABCD的面积=BC•AE=5×$\frac{5\sqrt{3}}{2}$=$\frac{25\sqrt{3}}{2}$;
故答案为:$\frac{25\sqrt{3}}{2}$.
点评 本题考查了菱形的性质、三角函数以及菱形面积的计算方法;通过解直角三角形求出菱形的高是解决问题的关键.

练习册系列答案
相关题目
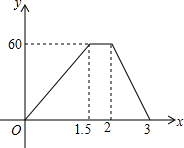 一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的函数关系如图所示.根据图象信息解答下列问题.
一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的函数关系如图所示.根据图象信息解答下列问题.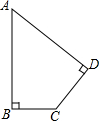 如图,已知一块四边形草地ABCD,其中∠A=45°,∠B=∠D=90°,AB=20m,CD=10m,求这块草地的面积.
如图,已知一块四边形草地ABCD,其中∠A=45°,∠B=∠D=90°,AB=20m,CD=10m,求这块草地的面积.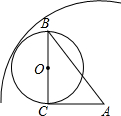 如图,Rt△ABC中,∠ACB=90°,BC=4cm,AC=3cm,⊙O是以BC为直径的圆,如果⊙O与⊙S相内切,那么⊙A的半径为$\sqrt{13}+2$cm.
如图,Rt△ABC中,∠ACB=90°,BC=4cm,AC=3cm,⊙O是以BC为直径的圆,如果⊙O与⊙S相内切,那么⊙A的半径为$\sqrt{13}+2$cm. 矩形ABCD四个内角平分线组成四边形MFNE,求证:四边形MFNE是正方形.
矩形ABCD四个内角平分线组成四边形MFNE,求证:四边形MFNE是正方形.