题目内容
5.某校九年级准备购买一批笔奖励优秀学生,在购买时发现,每只笔可以打九折,用360元钱购买的笔,打折后购买的数量比打折前多10本.(1)求打折前每支笔的售价是多少元?
(2)由于学生的需求不同,学校决定购买笔和笔袋共80件,笔袋每个原售价为10元,两种物品都打八折,若购买总金额不低于400元,问最多购买多少支笔?
分析 (1)根据打折后购买的数量比打折前多10本,进而得出等式求出答案;
(2)利用购买总金额不低于400元,得出不等关系进而求出答案.
解答 解:(1)设笔打折前售价为x,则打折后售价为0.9x,
由题意得:$\frac{360}{x}$+10=$\frac{360}{0.9x}$
解得:x=4,
经检验,x=4是原方程的根,
答:打折前每支笔的售价是4元;
(2)设购买笔y件,则购买笔袋80-y件,
由题意得:400≤4×0.8y+10×0.8×(80-y)
解得:y≤50,
答:最多购买50支笔.
点评 此题主要考查了分式方程的应用以及一元一次不等式的应用,正确得出等量关系是解题关键.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
16.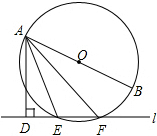 如图,已知直线l与⊙O相交于点E、F,AB是⊙O的直径,AD⊥l于点D,若∠DAE=22°,则∠BAF的大小为( )
如图,已知直线l与⊙O相交于点E、F,AB是⊙O的直径,AD⊥l于点D,若∠DAE=22°,则∠BAF的大小为( )
 如图,已知直线l与⊙O相交于点E、F,AB是⊙O的直径,AD⊥l于点D,若∠DAE=22°,则∠BAF的大小为( )
如图,已知直线l与⊙O相交于点E、F,AB是⊙O的直径,AD⊥l于点D,若∠DAE=22°,则∠BAF的大小为( )| A. | 12° | B. | 18° | C. | 22° | D. | 30° |
20.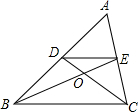 如图,点O是△ABC的重心,则C△DOE:C△BOC的值为( )
如图,点O是△ABC的重心,则C△DOE:C△BOC的值为( )
 如图,点O是△ABC的重心,则C△DOE:C△BOC的值为( )
如图,点O是△ABC的重心,则C△DOE:C△BOC的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{9}$ |
17.下列运算正确的是( )
| A. | $\sqrt{9}$=±3 | B. | (-a3)2=a6 | C. | a6÷a3=a2 | D. | (x+y)2=x2+y2 |
 倡导全民阅读,建设书香社会
倡导全民阅读,建设书香社会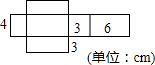 如图是一个长方体纸盒的展开图,这个纸盒的表面积是108cm2,体积是72cm3.
如图是一个长方体纸盒的展开图,这个纸盒的表面积是108cm2,体积是72cm3.