题目内容
20.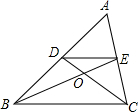 如图,点O是△ABC的重心,则C△DOE:C△BOC的值为( )
如图,点O是△ABC的重心,则C△DOE:C△BOC的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{9}$ |
分析 根据点O是△ABC的重心可知DE是△ABC的中位线,故可得出DE=$\frac{1}{2}$BC,再由重心的性质可知OD=$\frac{1}{2}$OC,OE=$\frac{1}{2}$OB,据此可得出结论.
解答 解:∵O是△ABC的重心,
∴DE是△ABC的中位线,OD=$\frac{1}{2}$OC,OE=$\frac{1}{2}$OB
∴DE=$\frac{1}{2}$BC,
∴C△DOE=DE+OD+OE=$\frac{1}{2}$(BC+OC+OB)=$\frac{1}{2}$C△BOC,
∴C△DOE:C△BOC=$\frac{1}{2}$.
故选A.
点评 本题考查的是三角形的重心,熟知重心到顶点的距离与重心到对边中点的距离之比为2:1是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.下列运算正确的是( )
| A. | x2•x=x2 | B. | 3x2-x2=2x2 | C. | (-3x)2=6x2 | D. | x8÷x4=x2 |
12.下列运算正确的是( )
| A. | -2(a-1)=-2a-1 | B. | (-2a)2=-2a2 | C. | (a-b)2=a2-b2 | D. | a6÷a2=a4 |
9. 如图,△ABC是直角三角形,AB⊥CD,图中与∠CAB互余的角有( )
如图,△ABC是直角三角形,AB⊥CD,图中与∠CAB互余的角有( )
 如图,△ABC是直角三角形,AB⊥CD,图中与∠CAB互余的角有( )
如图,△ABC是直角三角形,AB⊥CD,图中与∠CAB互余的角有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.点A的坐标为(2,3),点B的坐标为(-2,3),则点A与点B( )
| A. | 关于x轴对称 | B. | 关于y轴对称 | C. | 关于原点对称 | D. | 不是对称点 |