题目内容
14.根式$\frac{1}{{\sqrt{3}-\sqrt{2}}}$化为最简根式的结果是$\sqrt{3}$+$\sqrt{2}$.分析 分子和分母都乘以$\sqrt{3}$+$\sqrt{2}$,即可得出答案.
解答 解:$\frac{1}{\sqrt{3}-\sqrt{2}}$=$\frac{1×(\sqrt{3}+\sqrt{2})}{(\sqrt{3}-\sqrt{2})×(\sqrt{3}+\sqrt{2})}$=$\sqrt{3}$+$\sqrt{2}$,
故答案为:$\sqrt{3}$+$\sqrt{2}$.
点评 本题考查了分母有理化的应用,知道$\sqrt{3}$-$\sqrt{2}$的有理化因式是解此题的关键.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案
相关题目
9. 如图,△ABC是直角三角形,AB⊥CD,图中与∠CAB互余的角有( )
如图,△ABC是直角三角形,AB⊥CD,图中与∠CAB互余的角有( )
 如图,△ABC是直角三角形,AB⊥CD,图中与∠CAB互余的角有( )
如图,△ABC是直角三角形,AB⊥CD,图中与∠CAB互余的角有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,△ABC中,AB=AC=2,∠BAC=45°,将△ABC绕点A按顺时针方向旋转角α得到△AEF,且0°<α≤180°,连接BE、CF相交于点D.
如图,△ABC中,AB=AC=2,∠BAC=45°,将△ABC绕点A按顺时针方向旋转角α得到△AEF,且0°<α≤180°,连接BE、CF相交于点D.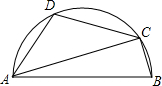 如图,AB是半圆的直径,C、D是半圆上的两点,且∠BAC=20°,则∠D=110°.
如图,AB是半圆的直径,C、D是半圆上的两点,且∠BAC=20°,则∠D=110°.