题目内容
8.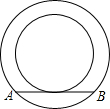 如图,两个同心圆的直径分别为6cm和10cm,大圆的一条弦AB与小圆相切,则弦AB的长为( )
如图,两个同心圆的直径分别为6cm和10cm,大圆的一条弦AB与小圆相切,则弦AB的长为( )| A. | 4cm | B. | 6cm | C. | 8cm | D. | 10cm |
分析 作OC⊥AB于C,连结OA,如图,根据切线的性质,由弦AB与小圆相切得到OC等于小圆的半径3cm,再利用勾股定理计算出AC=4,然后根据垂径定理得到AC=BC,则AB=2AC=8cm.
解答 解:作OC⊥AB于C,连结OA,如图,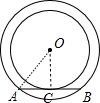
∵弦AB与小圆相切,
∴OC=3cm,
在Rt△OAC中,
∵OA=5,OC=3,
∴AC=$\sqrt{O{A}^{2}-O{C}^{2}}$=4,
∵OC⊥AB,
∴AC=BC,
∴AB=2AC=8cm.
故选:C.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了垂径定理和勾股定理.

练习册系列答案
相关题目
18.2014年7月5日,从山西省财政厅获悉,今年我省新增投资142亿元,用于改农村人居环境“四大工程”,该数据用科学记数法表示为( )
| A. | 1.42×109元 | B. | 1.42×1010元 | C. | 142×108元 | D. | 14.2×107元 |
19. 如图,∠A=∠D,AC=DF,下列条件中不能判断△ABC≌△DEF的是( )
如图,∠A=∠D,AC=DF,下列条件中不能判断△ABC≌△DEF的是( )
 如图,∠A=∠D,AC=DF,下列条件中不能判断△ABC≌△DEF的是( )
如图,∠A=∠D,AC=DF,下列条件中不能判断△ABC≌△DEF的是( )| A. | AB=DE | B. | ∠B=∠E | C. | EF=BC | D. | ∠F=∠C |
16.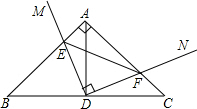 如图,在Rt直角△ABC中,∠B=45°,AB=AC,点D为BC中点,直角∠MDN绕点D旋转,DM,DN分别与边AB,AC交于E,F两点,下列结论:①△DEF是等腰直角三角形;②AE=CF;③△BDE≌△ADF;④BE+CF=EF,其中正确结论是( )
如图,在Rt直角△ABC中,∠B=45°,AB=AC,点D为BC中点,直角∠MDN绕点D旋转,DM,DN分别与边AB,AC交于E,F两点,下列结论:①△DEF是等腰直角三角形;②AE=CF;③△BDE≌△ADF;④BE+CF=EF,其中正确结论是( )
 如图,在Rt直角△ABC中,∠B=45°,AB=AC,点D为BC中点,直角∠MDN绕点D旋转,DM,DN分别与边AB,AC交于E,F两点,下列结论:①△DEF是等腰直角三角形;②AE=CF;③△BDE≌△ADF;④BE+CF=EF,其中正确结论是( )
如图,在Rt直角△ABC中,∠B=45°,AB=AC,点D为BC中点,直角∠MDN绕点D旋转,DM,DN分别与边AB,AC交于E,F两点,下列结论:①△DEF是等腰直角三角形;②AE=CF;③△BDE≌△ADF;④BE+CF=EF,其中正确结论是( )| A. | ①②④ | B. | ②③④ | C. | ①②③ | D. | ①②③④ |
17.已知m,n均不等于0,且m-n=2mn,则$\frac{2}{m}-\frac{2}{n}$的值是( )
| A. | 4 | B. | -4 | C. | $\frac{1}{4}$ | D. | -$\frac{1}{4}$ |
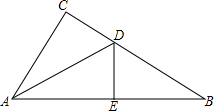 在△ABC中,∠C=90°,∠B=30°,AB的垂直平分线交BC于D,交AB于E,DB=12cm,则CD=6cm.
在△ABC中,∠C=90°,∠B=30°,AB的垂直平分线交BC于D,交AB于E,DB=12cm,则CD=6cm.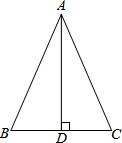 如图,等腰△ABC中,AB=AC=13cm,BC=10cm,求外接圆的半径.
如图,等腰△ABC中,AB=AC=13cm,BC=10cm,求外接圆的半径.