题目内容
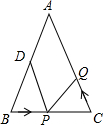 如图,在△ABC中,AB=AC=10,BC=8,点D为AB的中点,如果点P在线段BC上以每秒3个单位长度由B点向C点运动,同时点Q在线段CA上由C点向A点运动,当一个点停止运动时,另一个点也随之停止运动.在某一时刻,△BPD与△CQP全等,此时点Q的运动速度为每秒( )个单位长度.
如图,在△ABC中,AB=AC=10,BC=8,点D为AB的中点,如果点P在线段BC上以每秒3个单位长度由B点向C点运动,同时点Q在线段CA上由C点向A点运动,当一个点停止运动时,另一个点也随之停止运动.在某一时刻,△BPD与△CQP全等,此时点Q的运动速度为每秒( )个单位长度.| A、3 | ||
B、
| ||
| C、3或3.75 | ||
| D、2或3 |
考点:全等三角形的判定
专题:动点型
分析:设当△BPD与△CQP全等时点Q的运动速度为每秒x个单位长度,时间为t,求出BD,求出∠B=∠C,根据全等三角形的判定得出两种情况,分别求出即可.
解答:解:设当△BPD与△CQP全等时点Q的运动速度为每秒x个单位长度,时间为t,
∵AB=AC,
∴∠B=∠C,
∵AB=10,D为AB的中点,
∴BD=5,
要使△BPD与△CQP全等有两种情况:①BD=CP,BP=CQ,
即3t=xt,
解得:x=3;
②BD=CQ,BP=CP,
即5=xt,3t=8-3t,
解得:t=
,x=
=3.75,
故选C.
∵AB=AC,
∴∠B=∠C,
∵AB=10,D为AB的中点,
∴BD=5,
要使△BPD与△CQP全等有两种情况:①BD=CP,BP=CQ,
即3t=xt,
解得:x=3;
②BD=CQ,BP=CP,
即5=xt,3t=8-3t,
解得:t=
| 4 |
| 3 |
| 15 |
| 4 |
故选C.
点评:本题考查了全等三角形的性质和判定,等腰三角形的性质的应用,解此题的关键是求出符合情况的所有情况,注意全等三角形的判定定理有SAS,ASA,AAS,SSS.

练习册系列答案
相关题目
 如图,AB是⊙O的直径,C在⊙O上,若以B为圆心,BC为半径作⊙B,则直线AC与⊙B( )
如图,AB是⊙O的直径,C在⊙O上,若以B为圆心,BC为半径作⊙B,则直线AC与⊙B( )| A、相离 | B、相切 |
| C、相交 | D、相切或相交 |
 如图,在?ABCD中,点E为CD的中点,连接BE并延长交AD的延长线于点F.求证:点E是BF的中点,点D是AF的中点.
如图,在?ABCD中,点E为CD的中点,连接BE并延长交AD的延长线于点F.求证:点E是BF的中点,点D是AF的中点. 有一块薄铁皮ABCD,∠B=90°,各边的尺寸如图所示,若对角线AC剪开,得到的两块都是“直角三角形”形状吗?为什么?
有一块薄铁皮ABCD,∠B=90°,各边的尺寸如图所示,若对角线AC剪开,得到的两块都是“直角三角形”形状吗?为什么? 如图所示,在△ABC中,AB=AC,DE垂直平分AB于点E,交AC于点D,若△ABC的周长为26,BC=6,求△BCD的周长.
如图所示,在△ABC中,AB=AC,DE垂直平分AB于点E,交AC于点D,若△ABC的周长为26,BC=6,求△BCD的周长.