题目内容
 如图,在?ABCD中,点E为CD的中点,连接BE并延长交AD的延长线于点F.求证:点E是BF的中点,点D是AF的中点.
如图,在?ABCD中,点E为CD的中点,连接BE并延长交AD的延长线于点F.求证:点E是BF的中点,点D是AF的中点.考点:平行四边形的性质,全等三角形的判定与性质
专题:证明题
分析:由在?ABCD中,点E为CD的中点,易证得△BCE≌△FDE(AAS),然后由全等三角形的对应边相等,证得结论.
解答:证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠CBE=∠F,
∵点E为CD的中点,
∴CE=DE,
在△BCE和△FDE中,
,
∴△BCE≌△FDE(AAS),
∴BE=FE,BC=DF,
∴AD=DF,
即点E是BF的中点,点D是AF的中点.
∴AD∥BC,AD=BC,
∴∠CBE=∠F,
∵点E为CD的中点,
∴CE=DE,
在△BCE和△FDE中,
|
∴△BCE≌△FDE(AAS),
∴BE=FE,BC=DF,
∴AD=DF,
即点E是BF的中点,点D是AF的中点.
点评:此题考查了平行四边形的性质以及全等三角形的判定与性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )| A、a>0 |
| B、当x≥1时,y随x的增大而增大 |
| C、c<0 |
| D、当-1<x<3时,y>0 |
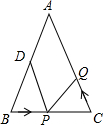 如图,在△ABC中,AB=AC=10,BC=8,点D为AB的中点,如果点P在线段BC上以每秒3个单位长度由B点向C点运动,同时点Q在线段CA上由C点向A点运动,当一个点停止运动时,另一个点也随之停止运动.在某一时刻,△BPD与△CQP全等,此时点Q的运动速度为每秒( )个单位长度.
如图,在△ABC中,AB=AC=10,BC=8,点D为AB的中点,如果点P在线段BC上以每秒3个单位长度由B点向C点运动,同时点Q在线段CA上由C点向A点运动,当一个点停止运动时,另一个点也随之停止运动.在某一时刻,△BPD与△CQP全等,此时点Q的运动速度为每秒( )个单位长度.| A、3 | ||
B、
| ||
| C、3或3.75 | ||
| D、2或3 |
 如果二次函数y=ax2+bx+c的图象如图所示,那么下列判断中,不正确的是( )
如果二次函数y=ax2+bx+c的图象如图所示,那么下列判断中,不正确的是( )| A、a>0 |
| B、b>0 |
| C、c<0 |
| D、b2-4ac>0 |
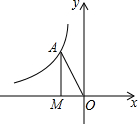 如图,若点A在反比例函数y=
如图,若点A在反比例函数y=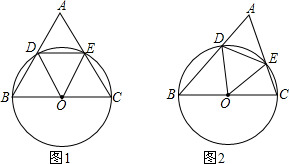
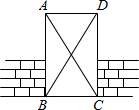 如图所示,工人师傅将门砌到一定高度时,质检员要测一下门的四个角是否都为直角,请你帮质检员想一个检测的办法,并说明理由.
如图所示,工人师傅将门砌到一定高度时,质检员要测一下门的四个角是否都为直角,请你帮质检员想一个检测的办法,并说明理由. 如图,BD是∠ABC的平分线,DF⊥BC于点F,S△ABC=36cm2,BC=18cm,AB=12cm,则DF的长是
如图,BD是∠ABC的平分线,DF⊥BC于点F,S△ABC=36cm2,BC=18cm,AB=12cm,则DF的长是