题目内容
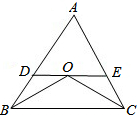 如图,∠ABC和∠ACB的平分线交于点O,DE经过点O且平行于BC,分别与AB、AC交于点D、E.
如图,∠ABC和∠ACB的平分线交于点O,DE经过点O且平行于BC,分别与AB、AC交于点D、E.(1)若∠ABC=50°,∠ACB=60°,求∠BOC的度数;
(2)∠ABC=a,∠ACB=b,用a、b的代数式表示∠BOC的度数.
考点:平行线的性质
专题:
分析:(1)先根据角平分线的定义得出∠OBC与∠OCB的度数,再由三角形内角和定理即可得出结论;
(2)先根据角平分线的定义用a、b表示出∠OBC与∠OCB的度数,再由三角形内角和定理即可得出结论.
(2)先根据角平分线的定义用a、b表示出∠OBC与∠OCB的度数,再由三角形内角和定理即可得出结论.
解答:解:(1)∵∠ABC和∠ACB的平分线交于点O,∠ABC=50°,∠ACB=60°,
∴∠OBC=
∠ABC=
×50°=25°,∠OCB=
∠ACB=
×60°=30°,
∴∠BOC=180°-25°-30°=125°;
(2))∵∠ABC和∠ACB的平分线交于点O,∠ABC=a,∠ACB=b,
∴∠OBC=
∠ABC=
a,∠OCB=
∠ACB=
b,
∴∠BOC=180°-
a-
b.
∴∠OBC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=180°-25°-30°=125°;
(2))∵∠ABC和∠ACB的平分线交于点O,∠ABC=a,∠ACB=b,
∴∠OBC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=180°-
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
相关题目
下列说法中,正确的是( )
| A、有一条公共边的两个全等三角形关于共边所在的直线对称 |
| B、全等三角形是关于某直线对称的 |
| C、两个图形关于某直线对称,则这两个图形一定分别位于这条直线的两侧 |
| D、关于某直线对称的两个三角形是全等三角形 |
计算:22010×(-
)2009的结果为( )
| 1 |
| 2 |
| A、2 | ||
B、
| ||
| C、-2 | ||
D、-
|
下列命题属于真命题的是( )
| A、同位角相等 |
| B、底边相等的两个等腰三角形全等 |
| C、到线段两个端点距离相等的点,一定在线段的中垂线上 |
| D、在角的内部,到角两边的距离相等的点,不一定在这个角的平分线上 |
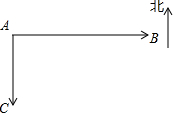 如图,甲船以15千米/时的速度从港口A向正南方向航行,乙船以20千米/时的速度,同时从港口A向正东方向航行.行驶2小时后,两船相距多远?
如图,甲船以15千米/时的速度从港口A向正南方向航行,乙船以20千米/时的速度,同时从港口A向正东方向航行.行驶2小时后,两船相距多远?