题目内容
17.若m<-1,则下列函数:①y=$\frac{m}{x}({x≥0})$;②y=-mx+1; ③y=mx; ④y=(m+1)x中,y随x增大而增大的是①③.分析 根据a的取值范围确定所有函数的比例系数的值,从而确定其增减性.
解答 解:∵m<-1,
∴-m>0,m+1<0,
∴y=$\frac{m}{x}({x≥0})$;②y=-mx+1; ③y=mx; ④y=(m+1)x中中y随x的增大而增大的有:①③.
故答案为:①③.
点评 本题考查了反比例函数、一次函数及正比例函数的性质,解题的关键是对有关函数的性质有熟练的掌握,难度不大.

练习册系列答案
相关题目
2.体育委员统计了全班同学60秒跳绳的次数,并列出下面的频数分布表:
从表中可知,组距和组数分别是( )
| 次数(x) | 60≤x<80 | 80≤x<100 | 100≤x<120 | 120≤x<140 | 140≤x<160 | 160≤x<180 | 180≤x<200 |
| 频数(人数) | 2 | 4 | 21 | 13 | 8 | 4 | 1 |
| A. | 组距8,组数20 | B. | 组距20,组数7 | C. | 组距7,组数20 | D. | 组距40,组数7 |
9.下列式子中,属于最简二次根式的是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{\frac{2}{3}}$ | C. | $\sqrt{0.3}$ | D. | $\sqrt{7}$ |
7.已知三角形的两边a=3,b=7,第三边是c,则c的取值范围是( )
| A. | 4<c<7 | B. | 7<c<10 | C. | 4<c<10 | D. | 7<c<13 |
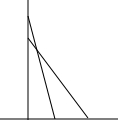 一架云梯长25m,如图那样斜靠在一面墙上,云梯底端离墙7m
一架云梯长25m,如图那样斜靠在一面墙上,云梯底端离墙7m