题目内容
7.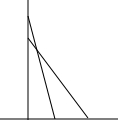 一架云梯长25m,如图那样斜靠在一面墙上,云梯底端离墙7m
一架云梯长25m,如图那样斜靠在一面墙上,云梯底端离墙7m(1)这架云梯的顶端距底面有多高?
(2)如果云梯的顶端下滑了4m,那么它的底部在水平方向也滑动了4m吗?
分析 (1)在直角三角形ADE中,利用勾股定理即可求出AE的长;
(2)首先求出A′E的长,利用勾股定理可求出D′E的长,进而得到DD′=ED′-ED的值.
解答  解:(1)在Rt△ADE中,由勾股定理得AE2+DE2=AD2,
解:(1)在Rt△ADE中,由勾股定理得AE2+DE2=AD2,
即AE2+72=252,
所以AE=24(m),
即这架云梯的顶端AE距地面有24 m高;
(2)梯子的底端在水平方向滑动了8m.
理由:∵云梯的顶端A下滑了4m至点A′,
∴A′E=AE-AA′=24-4=20(m),
在Rt△A′ED′中,由勾股定理得A′E2+DE′2=A′D′2,
即202+D′E2=252
所以D′E=15(m)
DD′=ED′-ED=15-7=8(m),
即梯子的底端在水平方向也滑动了8m.
点评 本题考查了勾股定理在实际生活中的应用,本题中根据梯子长不会变的等量关系求解是解题的关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
17.方程x2+x=12的根为( )
| A. | 4或3 | B. | -4或-3 | C. | -3或4 | D. | -4或3 |
 如图,△ABC绕点A旋转至△ADE的位置,点C在DE上,则△ABC≌△ADE,若∠EAC=38°,则∠E=71°.
如图,△ABC绕点A旋转至△ADE的位置,点C在DE上,则△ABC≌△ADE,若∠EAC=38°,则∠E=71°.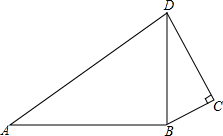 如图,在四边形ABCD中,AB=10cm,BC=2cm,CD=4cm,∠C=90°.
如图,在四边形ABCD中,AB=10cm,BC=2cm,CD=4cm,∠C=90°.