题目内容
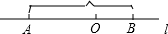
如图,直线l上有AB两点,AB=12cm,点O是线段AB上的一点,OA=2OB
(1)OA= cm OB= cm;
(2)若点C是线段AB上一点,且满足AC=CO+CB,求CO的长;
(3)若动点P,Q分别从A,B同时出发,向右运动,点P的速度为2cm/s,点Q的速度为1cm/s.设运动时间为ts,当点P与点Q重合时,P,Q两点停止运动.
①当t为何值时,2OP-OQ=4;
②当点P经过点O时,动点M从点O出发,以3cm/s的速度也向右运动.当点M追上点Q后立即返回,以3cm/s的速度向点P运动,遇到点P后再立即返回,以3cm/s的速度向点Q运动,如此往返,知道点P,Q停止时,点M也停止运动.在此过程中,点M行驶的总路程是多少?
(1)OA=
(2)若点C是线段AB上一点,且满足AC=CO+CB,求CO的长;
(3)若动点P,Q分别从A,B同时出发,向右运动,点P的速度为2cm/s,点Q的速度为1cm/s.设运动时间为ts,当点P与点Q重合时,P,Q两点停止运动.
①当t为何值时,2OP-OQ=4;
②当点P经过点O时,动点M从点O出发,以3cm/s的速度也向右运动.当点M追上点Q后立即返回,以3cm/s的速度向点P运动,遇到点P后再立即返回,以3cm/s的速度向点Q运动,如此往返,知道点P,Q停止时,点M也停止运动.在此过程中,点M行驶的总路程是多少?

考点:一元一次方程的应用,数轴
专题:
分析:(1)由于AB=12cm,点O是线段AB上的一点,OA=2OB,则OA+OB=3OB=AB=12cm,依此即可求解;
(2)根据图形可知,点C是线段AO上的一点,可设CO的长是xcm,根据AC=CO+CB,列出方程求解即可;
(3)①分0≤t<4;4≤t<6;t≥6三种情况讨论求解即可;
②求出点P经过点O到点P,Q停止时的时间,再根据路程=速度×时间即可求解.
(2)根据图形可知,点C是线段AO上的一点,可设CO的长是xcm,根据AC=CO+CB,列出方程求解即可;
(3)①分0≤t<4;4≤t<6;t≥6三种情况讨论求解即可;
②求出点P经过点O到点P,Q停止时的时间,再根据路程=速度×时间即可求解.
解答:解:(1)∵AB=12cm,OA=2OB,
∴OA+OB=3OB=AB=12cm,解得OB=4cm,
OA=2OB=8cm.
故答案为:8,4;
(2)设CO的长是xcm,依题意有
8-x=x+4+x,
解得x=
.
故CO的长是
cm;
(3)①当0≤t<4时,依题意有
2(8-2t)-(4+t)=4,
解得t=1.6;
当4≤t<6时,依题意有
2(2t-8)-(4+t)=4,
解得t=8(不合题意舍去);
当t≥6时,依题意有
2(2t-8)-(4+t)=4,
解得t=8.
故当t为1.6s或8s时,2OP-OQ=4;
②[4+(8÷2)×1]÷(2-1)
=[4+4]÷1
=8(s),
3×8=24(cm).
答:点M行驶的总路程是24cm.
∴OA+OB=3OB=AB=12cm,解得OB=4cm,
OA=2OB=8cm.
故答案为:8,4;
(2)设CO的长是xcm,依题意有
8-x=x+4+x,
解得x=
| 4 |
| 3 |
故CO的长是
| 4 |
| 3 |
(3)①当0≤t<4时,依题意有
2(8-2t)-(4+t)=4,
解得t=1.6;
当4≤t<6时,依题意有
2(2t-8)-(4+t)=4,
解得t=8(不合题意舍去);
当t≥6时,依题意有
2(2t-8)-(4+t)=4,
解得t=8.
故当t为1.6s或8s时,2OP-OQ=4;
②[4+(8÷2)×1]÷(2-1)
=[4+4]÷1
=8(s),
3×8=24(cm).
答:点M行驶的总路程是24cm.
点评:本题考查了数轴及数轴的三要素(正方向、原点和单位长度).一元一次方程的应用以及数轴上两点之间的距离公式的运用,行程问题中的路程=速度×时间的运用.注意(3)①需要分类讨论.

练习册系列答案
相关题目
在十二点三十分时,钟表上的时针与分针所成的角( )
| A、直角 | B、钝角 | C、平角 | D、锐角 |
在等式x2( )=x7中,括号里的代数式为( )
| A、x2 |
| B、x3 |
| C、x4 |
| D、x5 |
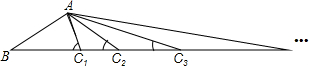 如图,在△ABC1中,∠AC1B=80°,以C1为顶点作等腰△AC1C2,再以C2为顶点作等腰△AC2C3,…以C3=1为顶点作若腰△ACn-1Cn,则∠ACnB等于
如图,在△ABC1中,∠AC1B=80°,以C1为顶点作等腰△AC1C2,再以C2为顶点作等腰△AC2C3,…以C3=1为顶点作若腰△ACn-1Cn,则∠ACnB等于
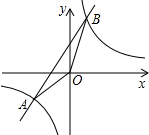 如图,已知A(-2,-2)、B(n,4)是一次函数y=kx+b的图象和反比例函数y=
如图,已知A(-2,-2)、B(n,4)是一次函数y=kx+b的图象和反比例函数y= 画出下列几何体的三视图.
画出下列几何体的三视图.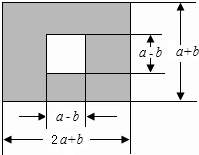 如图,某地有块长为(2a+b)米,宽为(a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将搞一雕塑.
如图,某地有块长为(2a+b)米,宽为(a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将搞一雕塑.