题目内容
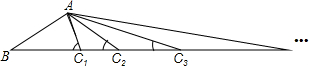 如图,在△ABC1中,∠AC1B=80°,以C1为顶点作等腰△AC1C2,再以C2为顶点作等腰△AC2C3,…以C3=1为顶点作若腰△ACn-1Cn,则∠ACnB等于
如图,在△ABC1中,∠AC1B=80°,以C1为顶点作等腰△AC1C2,再以C2为顶点作等腰△AC2C3,…以C3=1为顶点作若腰△ACn-1Cn,则∠ACnB等于考点:等腰三角形的性质
专题:规律型
分析:根据等腰三角形的性质和三角形外角的性质即可求得结果.
解答:解:∵以C1为顶点作等腰△AC1C2,
∴∠AC2C1=∠C1AC2,
∵∠AC1B=80°,
∴∠AC2C1=40°,
∵以C2为顶点作等腰△AC2C3,
∴AC2=C2C3,
∴∠AC3C2=∠C2AC3,
∴∠AC3C1=20°,
…
∴∠ACnB=
.
故答案为
.
∴∠AC2C1=∠C1AC2,
∵∠AC1B=80°,
∴∠AC2C1=40°,
∵以C2为顶点作等腰△AC2C3,
∴AC2=C2C3,
∴∠AC3C2=∠C2AC3,
∴∠AC3C1=20°,
…
∴∠ACnB=
| 80° |
| 2n-1 |
故答案为
| 80° |
| 2n-1 |
点评:本题考查了等腰三角形的性质以及三角形外角的性质,关键是找出规律.

练习册系列答案
相关题目
若-a2bm与
anb5是同类项,则m,n的值分别为( )
| 8 |
| 7 |
| A、2和5 | B、5和2 |
| C、4和1 | D、1和4 |
由四舍五入法得到的近似数2.37×103,下列说法正确的是( )
| A、精确到百分位 |
| B、精确到个位 |
| C、精确到十位 |
| D、精确到千位 |
一个扇形的圆心角为120°,半径为15cm,则它的弧长为( )
| A、5πcm | B、10πcm |
| C、15πcm | D、20πcm |
 如图,直线a∥b.直线c与直线a,b分别相交于点A、点B,AM⊥b,垂足为点M,若∠1=32°,则∠2=
如图,直线a∥b.直线c与直线a,b分别相交于点A、点B,AM⊥b,垂足为点M,若∠1=32°,则∠2=