题目内容
19.在四边形ABCD中,AC、BD交于点E,且∠ACD=∠ADC.(1)如图1,若AB=AD,求证:∠BAC=2∠BDC;
(2)如图2,在(1)的条件下,若∠BDC=30°,求证:BC=AC.
(3)如图3,若BC=AD,∠BDC=30°,过A作AH⊥BD于H,过C作CF⊥BD于F,且HF:BH=2:11,DF=9,求BD的长.
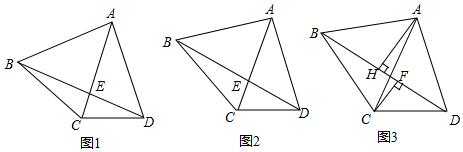
分析 (1)如图1,根据AB=AD=AC,作辅助圆A,由∠BAC与∠BDC是$\widehat{BC}$所对的圆心角和圆周角,所以∠BAC=2∠BDC;
(2)根据同弧所对的圆心角是圆周角的二倍可得:△ABC是等边三角形,所以BC=AC;
(3)如图3,作辅助线,根据等腰三角形三线合一得:CE=ED=$\frac{1}{2}$CD,由直角三角形30°角的性质得:CF=$\frac{1}{2}$CD,则CE=CF,利用HL证明Rt△ACE≌Rt△BCF,得∠DCF=∠ACB=60°,则△ABC是等边三角形,
设HF=2x,BH=11x,由BH=HD列方程可得结论.
解答 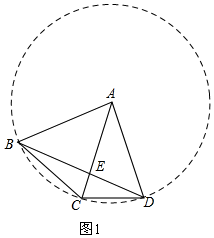 解:(1)如图1,∵∠ACD=∠ADC,
解:(1)如图1,∵∠ACD=∠ADC,
∴AC=AD,
∵AB=AD,
∴AB=AD=AC,
∴点B,C,D三点在以A为圆心,以AB为半径的圆上,
∵∠BAC与∠BDC是$\widehat{BC}$所对的圆心角和圆周角,
∴∠BAC=2∠BDC;
(2)由(1)证得:∠BAC=2∠BDC,
∵∠BDC=30°,
∴∠BAC=60°,
∵AB=AC,
∴△ABC是等边三角形,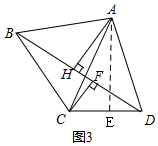
∴BC=AC;
(3)如图3,过A作AE⊥CD于E,
∵AC=AD,
∴CE=ED=$\frac{1}{2}$CD,
∵∠BCD=30°,
∴CF=$\frac{1}{2}$CD,
∴CE=CF,
∵BC=AD=AC,∠AEC=∠BFC=90°,
∴Rt△ACE≌Rt△BCF(HL),
∴∠ACE=∠BCF,
∴∠ACE-∠ACF=∠BCF-∠ACF,
即∠DCF=∠ACB=60°,
∵AC=BC,
∴△ABC是等边三角形,
∴BC=AB,
∴AD=AB,
∵AH⊥BD,
∴BH=HD,
∵HF:BH=2:11,DF=9,
设HF=2x,BH=11x,
由BH=HD得:11x=2x+9,
x=1,
∴BD=11x+2x+9=22.
点评 本题是四边形的综合题,考查了等腰三角形的性质、直角三角形30°角的性质,圆周角定理、三角形性质和判定,利用圆的半径都相等,构建辅助圆,利用同弧所对的圆周角与圆心角的关系解决问题,第3问有难度,构建辅助线,证明Rt△ACE≌Rt△BCF是关键.

 阅读快车系列答案
阅读快车系列答案| A. | 7 | B. | 11 | C. | -7 | D. | -11 |
| A. |  | B. |  | C. |  | D. |  |
| A. |  | B. |  | C. |  | D. |  |
| A. | -6+2b-3a+ab | B. | -6-2b+3a+ab | C. | ab-3b+2a-6 | D. | ab-2a+3b-6 |
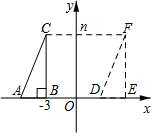 如图,直角三角形的顶点A、B在x轴上,∠ABC=90°,BC∥y轴,且C点在第二象限,B点为(-3,0),将直角三角形ABC沿x轴水平向右平移m个单位,得到对应的直角三角形DEF,其中点A、B、C分别对应点D、E、F,求:
如图,直角三角形的顶点A、B在x轴上,∠ABC=90°,BC∥y轴,且C点在第二象限,B点为(-3,0),将直角三角形ABC沿x轴水平向右平移m个单位,得到对应的直角三角形DEF,其中点A、B、C分别对应点D、E、F,求: