题目内容
11.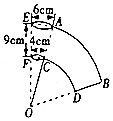 如图所示是一个纸杯,它的母线延长后形成的立体图形是圆锥,该圆锥的侧面展开图是扇形OAB,经测量,纸杯开口圆的直径为6cm,下底面直径为4cm,母线长EF=9cm,求扇形OAB的圆心角及这个纸杯的表面积.(结果保留根号和π)
如图所示是一个纸杯,它的母线延长后形成的立体图形是圆锥,该圆锥的侧面展开图是扇形OAB,经测量,纸杯开口圆的直径为6cm,下底面直径为4cm,母线长EF=9cm,求扇形OAB的圆心角及这个纸杯的表面积.(结果保留根号和π)
分析 (1)设∠AOB=n°,AO=R,则CO=R-9,利用圆锥的侧面展开图扇形的弧长等于圆锥底面周长作为相等关系列方程,并联立成方程组求解即可;
(2)求纸杯的侧面积即为扇环的面积,需要用大扇形的面积减去小扇形的面积.纸杯表面积=S纸杯侧面积+S纸杯底面积.
解答 解:由题意可知:$\widehat{BA}$=6πcm,$\widehat{CD}$=4π,设∠AOB=n,AO=R,则CO=R-9,
由弧长公式得:l=$\frac{nπR}{180}$,
∴$\left\{\begin{array}{l}{6×180=nR}\\{4×180=nR-9n}\end{array}\right.$,
解得:n=40,R=27,
故扇形OAB的圆心角是40度.
∵R=27,R-9=18,
∴S扇形OCD=$\frac{1}{2}$×4π×18=36π(cm2),
S扇形OAB=$\frac{1}{2}$×6π×27=81π(cm2),
纸杯侧面积=S扇形OAB-S扇形OCD=81π-36π=45π(cm2),
纸杯底面积=π•22=4π(cm2)
纸杯表面积=45π+4π=49π(cm2).
点评 此题主要考查圆锥的侧面展开图与底面周长之间的关系和扇环的面积的求法.本题中(1)就是把的扇形的弧长等于圆锥底面周长作为相等关系,列方程求解;(2)扇环的面积等于大扇形的面积减去小扇形的面积.

练习册系列答案
相关题目
2.在下面各图中,∠1=∠2,能判断AB∥CD的是( )
| A. |  | B. |  | ||
| C. | 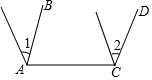 | D. | 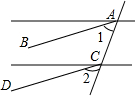 |
 如图,矩形ABCD中,E是BC上一点,且$\frac{BE}{EC}$=4,AE⊥DE,求$\frac{AB}{BC}$的值.
如图,矩形ABCD中,E是BC上一点,且$\frac{BE}{EC}$=4,AE⊥DE,求$\frac{AB}{BC}$的值. 如图,已知∠AOB和点C,D,请用直尺和圆规准确作出点P,使它到∠AOB的两边距离相等,且PC=PD.(不写作法,保留作图痕迹)
如图,已知∠AOB和点C,D,请用直尺和圆规准确作出点P,使它到∠AOB的两边距离相等,且PC=PD.(不写作法,保留作图痕迹) 已知,y=-$\frac{4}{3}$x+4与x轴,y轴的交点分别是点A,B,点C(-2,3),O是原点,求点C到直线AB的距离.
已知,y=-$\frac{4}{3}$x+4与x轴,y轴的交点分别是点A,B,点C(-2,3),O是原点,求点C到直线AB的距离. 如图,已知△ABC,请用尺规作△ABC的中位线EF,使EF∥BC.
如图,已知△ABC,请用尺规作△ABC的中位线EF,使EF∥BC.