题目内容
16.过⊙O内一点M最长的弦长为4cm,最短的弦长为2cm,则OM=$\sqrt{3}$cm.分析 圆内最长的弦为直径,最短的弦是过点M且与这条直径垂直的弦,由勾股定理和垂径定理求解即可.
解答  解:如图所示,
解:如图所示,
∵AB=4cm,CD=2cm,
∴由垂径定理:OC=2cm,CM=1cm,
∴由勾股定理得:OM=$\sqrt{O{C}^{2}-C{M}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$(cm),
故答案为:$\sqrt{3}$.
点评 本题综合考查了垂径定理和勾股定理.解此类题目要注意将圆的问题转化成三角形的问题再进行计算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.如图,有四个大小相同的小长方形和两个大小相同的大长方形按如图位置摆放,按照图中所示尺寸,则小长方形的长与宽的差是( )
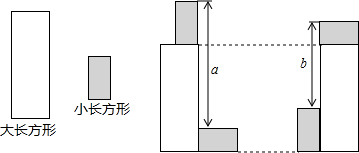

| A. | 3b-2a | B. | $\frac{a-b}{2}$ | C. | $\frac{a-b}{3}$ | D. | $\frac{a}{3}-\frac{b}{4}$ |
11.如果m是任意实数,那么点M(m-5,m+2)一定不在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
8.下列标志是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
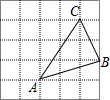 如图,每个小方格都是边长为1个单位的小正方形,A,B,C三点都是格点(每个小方格的顶点叫格点).
如图,每个小方格都是边长为1个单位的小正方形,A,B,C三点都是格点(每个小方格的顶点叫格点). 如图是由5个大小相同的小正方体摆成的立体图形,则从正面看得到的平面图形是( )
如图是由5个大小相同的小正方体摆成的立体图形,则从正面看得到的平面图形是( )



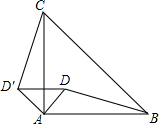 如图,D是等腰Rt△ABC内一点,BC是斜边,如果将△ABD绕点A逆时针方向旋转到△ACD′的位置,则∠ADD′=45°.
如图,D是等腰Rt△ABC内一点,BC是斜边,如果将△ABD绕点A逆时针方向旋转到△ACD′的位置,则∠ADD′=45°.