题目内容
9.正比例函数y1=k1x与反比例函数y2=$\frac{{k}_{2}}{x}$的图象相交于A,B两点.若点A的坐标为(2,1),则当y1>y2时,x的取值范围是-2<x<0或x>2.分析 根据正比例函数与反比例函数图象的对称性可知:A与B关于原点对称,从而可求出点B的坐标,然后结合图象就可解决问题.
解答 解:∵正比例函数y1=k1x与反比例函数y2=$\frac{{k}_{2}}{x}$的图象都是以原点为中心的中心对称图形,
∴它们的交点A、B关于原点成中心对称,
∵点A的坐标为(2,1),
∴点B的坐标为(-2,-1).
如图所示:
结合图象可得:当y1>y2时,x的取值范围是-2<x<0或x>2.
故答案为-2<x<0或x>2.
点评 本题考查的是有关正比例函数与反比例函数图象交点问题,运用数形结合的思想是解决本题的关键.

练习册系列答案
相关题目
19.下列事件中,属于必然事件的是( )
| A. | 明天我市下雨 | |
| B. | 抛一枚硬币,正面朝上 | |
| C. | 我走出校门,看到的第一辆汽车的牌照的末位数字是偶数 | |
| D. | 一个口袋中装有2个红球和一个白球,从中摸出2个球,其中有红球 |
4.某通讯公司推出移动电话的两种计费方式(详请见下表)
温馨提示:若选用方式一,每月固定交费58元,当主动打出电话月累计时间不超过150分,不再额外交费;当超过150分,超过部分加收0.25元.
设一个月内使用移动电话主叫的时间为t分(t为正整数),
请根据表中提供的信息回答下列问题:
(1)用含有t的式子填写下表:
(2)当t=270时,哪种计费方式更省钱?请通过计算说明你的理由.
(3)当t>350时,请选择哪一种说法最合理B
A.方式一计费省钱 B.方式二计费省钱
C.两种方式计费相同 D.无法判定.
| 固定交费 | 主叫限定 时间/分 | 主叫超时费 (元/分) | 被叫 | |
| 方式一 | 58 | 150 | 0.25 | 免费 |
| 方式二 | 88 | 350 | 0.19 | 免费 |
设一个月内使用移动电话主叫的时间为t分(t为正整数),
请根据表中提供的信息回答下列问题:
(1)用含有t的式子填写下表:
| t≤150 | 150<t<350 | t=350 | t>350 | |
| 方式一计费/元 | 58 | 0.25t+20.5 | 108 | 0.25t+20.5 |
| 方式二计费/元 | 88 | 88 | 88 | 0.19t+21.5 |
(3)当t>350时,请选择哪一种说法最合理B
A.方式一计费省钱 B.方式二计费省钱
C.两种方式计费相同 D.无法判定.
14.已知一个数的倒数的绝对值等于这个数的相反数,则这个数是( )
| A. | 1 | B. | 0 | C. | -1或1 | D. | -1 |
1.已知反比例函数y=$\frac{k}{x}$(k≠0)的图象,在每一个象限内,y随x的增大而增大,则一次函数y=-kx+k的图象不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
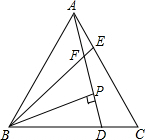 如图,已知△ABC为等边三角形,AE=CD,AD、BE相交于点F.
如图,已知△ABC为等边三角形,AE=CD,AD、BE相交于点F.