题目内容
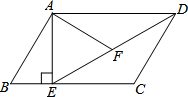 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为点E,连接DE,F为线段DE上一点,且∠AFE=∠B.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为点E,连接DE,F为线段DE上一点,且∠AFE=∠B.(1)求证:△ADF∽△DEC;
(2)若AB=4,AD=3
| 3 |
| 3 |
考点:相似三角形的判定与性质,勾股定理,平行四边形的性质
专题:
分析:(1)△ADF和△DEC中,易知∠ADF=∠CED(平行线的内错角),而∠AFD和∠C是等角的补角,由此可判定两个三角形相似;
(2)由(1)知△ADF∽△DEC,根据相似三角形的性质:对应边的比值相等即可求出DE的长,再利用勾股定理即可求出AE的长.
(2)由(1)知△ADF∽△DEC,根据相似三角形的性质:对应边的比值相等即可求出DE的长,再利用勾股定理即可求出AE的长.
解答:(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴∠B+∠C=180°,∠ADF=∠DEC.
∵∠AFD+∠AFE=180°,∠AFE=∠B
∴∠AFD=∠C
∴△ADF∽△DEC;
(2)解:∵四边形ABCD是平行四边形,
∴CD=AB=4,
由(1)知△ADF∽△DEC,
∴
=
,
∴DE=
=
=6.
在Rt△ADE中,由勾股定理得:AE=
=
=3.
∴AB∥CD,AD∥BC,
∴∠B+∠C=180°,∠ADF=∠DEC.
∵∠AFD+∠AFE=180°,∠AFE=∠B
∴∠AFD=∠C
∴△ADF∽△DEC;
(2)解:∵四边形ABCD是平行四边形,
∴CD=AB=4,
由(1)知△ADF∽△DEC,
∴
| AD |
| DE |
| AF |
| CD |
∴DE=
| AD•CD |
| AF |
3
| ||
2
|
在Rt△ADE中,由勾股定理得:AE=
| DE2-AD2 |
62-(3
|
点评:此题主要考查的是平行四边形的性质、相似三角形的判定和性质以及勾股定理的运用,解题的关键是熟记判定三角形相似的各种方法和各种性质.

练习册系列答案
相关题目
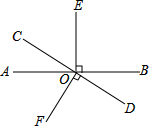 如图,直线AB与CD相交于O,OE⊥AB,OF⊥CD,
如图,直线AB与CD相交于O,OE⊥AB,OF⊥CD, 如图,线段AB=8cm,C是线段AB上一点,AC=3cm,M是AB的中点,N是AC的中点.
如图,线段AB=8cm,C是线段AB上一点,AC=3cm,M是AB的中点,N是AC的中点. (1)已知线段AB和直线CD,如图,画AB关于CD的轴对称图形;
(1)已知线段AB和直线CD,如图,画AB关于CD的轴对称图形;
 林业工人常用一种角卡为工具测大树的直径,其工作原理如图.现已知∠BAC=60°,AB=30cm,则这棵大树的直径为
林业工人常用一种角卡为工具测大树的直径,其工作原理如图.现已知∠BAC=60°,AB=30cm,则这棵大树的直径为