题目内容
 林业工人常用一种角卡为工具测大树的直径,其工作原理如图.现已知∠BAC=60°,AB=30cm,则这棵大树的直径为
林业工人常用一种角卡为工具测大树的直径,其工作原理如图.现已知∠BAC=60°,AB=30cm,则这棵大树的直径为考点:切线的性质,解直角三角形
专题:
分析:由切线的性质可知:∠ABO=90°,在直角三角形AOB中,运用三角函数定义求OB,即半径,由此求出树的直径.
解答:解:由题意可知:AB,AC是圆O的切线,
∴∠OAB=
∠BAC=
×60°=30°,
∵OB⊥AB,
∴∠ABO=90°,
∴OB=AB•tan∠OAB=30tan30°=10
cm,
∴树的直径为2OB=20
cm,
故答案为:20
.
∴∠OAB=
| 1 |
| 2 |
| 1 |
| 2 |
∵OB⊥AB,
∴∠ABO=90°,
∴OB=AB•tan∠OAB=30tan30°=10
| 3 |
∴树的直径为2OB=20
| 3 |
故答案为:20
| 3 |
点评:本题考查了切线的性质以及切线长定理,此题关键是把实际问题转化为数学问题,抽象到直角三角形中来考虑问题.

练习册系列答案
相关题目
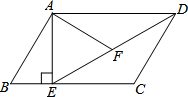 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为点E,连接DE,F为线段DE上一点,且∠AFE=∠B.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为点E,连接DE,F为线段DE上一点,且∠AFE=∠B. 如图,AB⊥EF于点G,CD⊥EF于点H,GP平分∠EGB,HQ平分∠CHF,则图中互相平行的直线有
如图,AB⊥EF于点G,CD⊥EF于点H,GP平分∠EGB,HQ平分∠CHF,则图中互相平行的直线有 如图,直线y=-
如图,直线y=-