题目内容
若一次函数y=2kx与y=kx+b(k≠0,b≠0)的图象相交于点(2,-4).
(1)求k、b的值;
(2)若点(m,n)在函数y=kx+b的图象上,求m2+2mn+n2的值.
(1)求k、b的值;
(2)若点(m,n)在函数y=kx+b的图象上,求m2+2mn+n2的值.
考点:两条直线相交或平行问题
专题:
分析:(1)把交点坐标代入y=2kx求出k,再代入y=kx+b求出b的值即可;
(2)把点(m,n)代入直线解析式求出m+n=-2,然后利用完全平方公式求解即可.
(2)把点(m,n)代入直线解析式求出m+n=-2,然后利用完全平方公式求解即可.
解答:解:(1)将点(2,-4)代入y=2kx得,
2k•2=-4,
解得k=-1,
代入y=kx+b得,-1×2+b=-4,
解得b=-2,
故,k=-1,b=-2;
(2)∵点(m,n)在函数y=kx+b的图象上,
∴-m-2=n,
∴m+n=-2,
m2+2mn+n2
=(m+n)2
=(-2)2
=4.
2k•2=-4,
解得k=-1,
代入y=kx+b得,-1×2+b=-4,
解得b=-2,
故,k=-1,b=-2;
(2)∵点(m,n)在函数y=kx+b的图象上,
∴-m-2=n,
∴m+n=-2,
m2+2mn+n2
=(m+n)2
=(-2)2
=4.
点评:本题考查了两直线相交的问题,(1)把交点坐标代入两个函数解析式计算即可,比较简单,(2)把点的坐标代入直线解析式正好得到m+n的形式是解题的关键.

练习册系列答案
相关题目
 作图:(保留作图痕迹,不要求写作法)
作图:(保留作图痕迹,不要求写作法) 如图,AB=CB,BE=BF,∠1=∠2,证明:△ABE≌△CBF.
如图,AB=CB,BE=BF,∠1=∠2,证明:△ABE≌△CBF.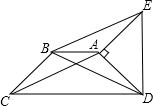 如图,在等腰梯形ABCD中,已知AB∥CD,AD=BC,∠ADC=45°,将腰AD绕A点逆时针旋转90°,得到AE,连接BE、DE、AC、BD.求证:四边形ACBE是平行四边形.
如图,在等腰梯形ABCD中,已知AB∥CD,AD=BC,∠ADC=45°,将腰AD绕A点逆时针旋转90°,得到AE,连接BE、DE、AC、BD.求证:四边形ACBE是平行四边形.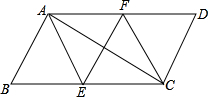 如图,?ABCD中,AE、CF分别是∠BAD和∠BCD的角平分线,根据现有的图形,请添加一个条件,使四边形AECF为菱形,则添加的一个条件可以是
如图,?ABCD中,AE、CF分别是∠BAD和∠BCD的角平分线,根据现有的图形,请添加一个条件,使四边形AECF为菱形,则添加的一个条件可以是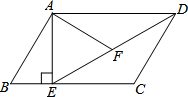 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为点E,连接DE,F为线段DE上一点,且∠AFE=∠B.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为点E,连接DE,F为线段DE上一点,且∠AFE=∠B.