题目内容
2. 如图所示,在△ABC中,AB=AC,BD=CD,DE⊥AB于E,DF⊥AC于F,G为边BC上与点B,D,C不重合的任意一点,GH⊥AB于H,GM⊥AC于M;求证:GH+GM=DE+DF.
如图所示,在△ABC中,AB=AC,BD=CD,DE⊥AB于E,DF⊥AC于F,G为边BC上与点B,D,C不重合的任意一点,GH⊥AB于H,GM⊥AC于M;求证:GH+GM=DE+DF.
分析 连接AD、AG,利用三角形的面积可得S△ABC=S△ADB+S△ACD=$\frac{1}{2}$AB•DE+$\frac{1}{2}$AC•DF,S△ABC=S△ABG+S△ACG=$\frac{1}{2}$AB•HG+$\frac{1}{2}$AC•GM,进而可得$\frac{1}{2}$AB•DE+$\frac{1}{2}$AC•DF=$\frac{1}{2}$AB•HG+$\frac{1}{2}$AC•GM,再由AB=AC可得结论.
解答  证明:连接AD、AG,
证明:连接AD、AG,
∵S△ABC=S△ADB+S△ACD=$\frac{1}{2}$AB•DE+$\frac{1}{2}$AC•DF,
S△ABC=S△ABG+S△ACG=$\frac{1}{2}$AB•HG+$\frac{1}{2}$AC•GM,
∴$\frac{1}{2}$AB•DE+$\frac{1}{2}$AC•DF=$\frac{1}{2}$AB•HG+$\frac{1}{2}$AC•GM,
∵AB=AC,
∴GH+GM=DE+DF.
点评 此题主要考查了等腰三角形的性质,以及三角形的面积,关键是正确运用不同的方法表示△ABC的面积.

练习册系列答案
相关题目
2.物体的速度V与阻力F成正比,当阻力为40牛时,速度为5米/秒,则V与F之间的函数关系为( )
| A. | V=8F | B. | FV=8 | C. | V=$\frac{1}{8}$F | D. | FV=$\frac{1}{8}$ |
7.若-3xmy4与7x2yn-1是同类项,则m+n的值为( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
12. 如图,已知平行四边形ABCD中,AC,BD相交于点O,AD=BD=8,AC=12,则△ADO的周长是( )
如图,已知平行四边形ABCD中,AC,BD相交于点O,AD=BD=8,AC=12,则△ADO的周长是( )
 如图,已知平行四边形ABCD中,AC,BD相交于点O,AD=BD=8,AC=12,则△ADO的周长是( )
如图,已知平行四边形ABCD中,AC,BD相交于点O,AD=BD=8,AC=12,则△ADO的周长是( )| A. | 20 | B. | 18 | C. | 16 | D. | 12 |
 将一副直角三角尺如图叠放,若∠AOD=15°,则∠BOC=165°.
将一副直角三角尺如图叠放,若∠AOD=15°,则∠BOC=165°.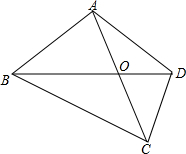 如图所示,四边形ABCD中,对角线AC、BD交于点O,且AB=AD,AO=OC,请你猜想AB+BO与BC+OD的数量关系,并证明你的结论.
如图所示,四边形ABCD中,对角线AC、BD交于点O,且AB=AD,AO=OC,请你猜想AB+BO与BC+OD的数量关系,并证明你的结论.