题目内容
11.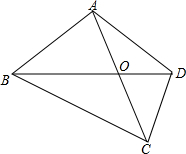 如图所示,四边形ABCD中,对角线AC、BD交于点O,且AB=AD,AO=OC,请你猜想AB+BO与BC+OD的数量关系,并证明你的结论.
如图所示,四边形ABCD中,对角线AC、BD交于点O,且AB=AD,AO=OC,请你猜想AB+BO与BC+OD的数量关系,并证明你的结论.
分析 分三种情况:若OB>DO,在BO上取点E使OE=OD,连接AE,CE,则四边形AECD是平行四边形,根据平行四边形的性质得到AD=CE,于是得到BC-AB=BC-AD=BC-CE<BE=OB-OE=OB-OD,即可求得AB+BO>BC+DO;②若OB<DO,同理得到AB+BO∠BC+OD,若OB=OD,同理得到AB+OB=BC+OD.
解答 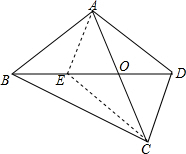 解:①若OB>DO,在BO上取点E使OE=OD,连接AE,CE,则四边形AECD是平行四边形,
解:①若OB>DO,在BO上取点E使OE=OD,连接AE,CE,则四边形AECD是平行四边形,
∴AD=CE,
∴BC-AB=BC-AD=BC-CE<BE=OB-OE=OB-OD,
∴AB+BO>BC+DO;
②若OB<DO,同理得到AB+BO∠BC+OD,
③若OB=OD,同理得到AB+OB=BC+OD.
点评 本题考查了平行四边形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
3. 如图,下列条件不能判断l1∥l2的是( )
如图,下列条件不能判断l1∥l2的是( )
 如图,下列条件不能判断l1∥l2的是( )
如图,下列条件不能判断l1∥l2的是( )| A. | 180°-∠4=∠2 | B. | ∠1=∠3 | C. | ∠4=∠5 | D. | ∠2+∠4=180° |
 如图所示,在△ABC中,AB=AC,BD=CD,DE⊥AB于E,DF⊥AC于F,G为边BC上与点B,D,C不重合的任意一点,GH⊥AB于H,GM⊥AC于M;求证:GH+GM=DE+DF.
如图所示,在△ABC中,AB=AC,BD=CD,DE⊥AB于E,DF⊥AC于F,G为边BC上与点B,D,C不重合的任意一点,GH⊥AB于H,GM⊥AC于M;求证:GH+GM=DE+DF. 如图,已知正方形ABCD的边长为3cm,以CD为边向CD的两旁分别作等边△PCD和等边△QCD.
如图,已知正方形ABCD的边长为3cm,以CD为边向CD的两旁分别作等边△PCD和等边△QCD.